Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

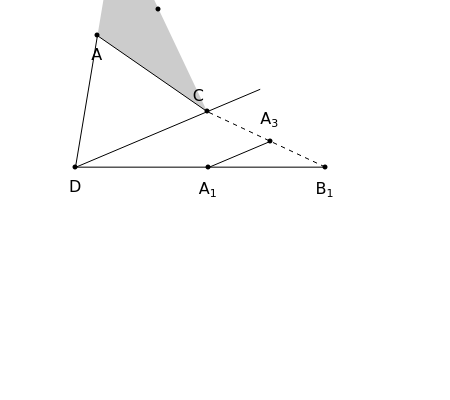
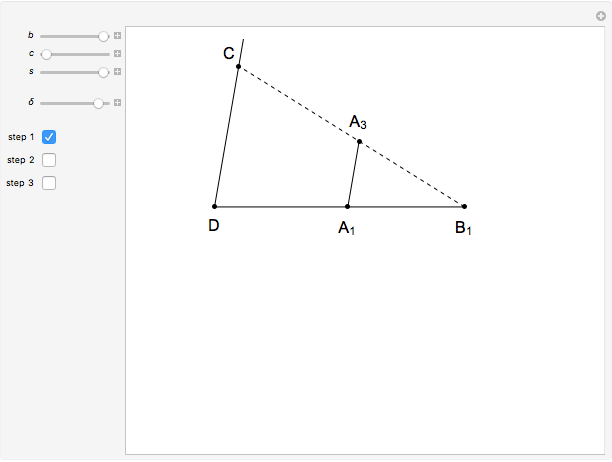
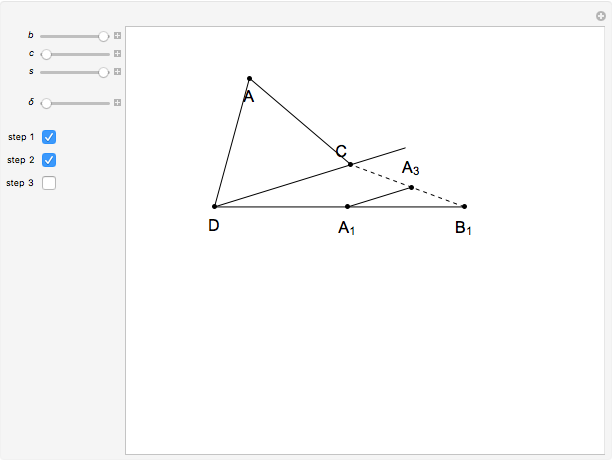
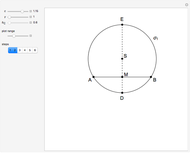
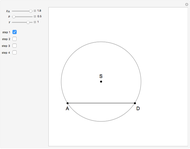
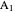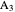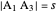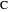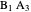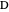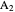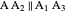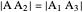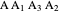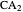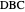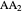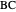11b. Construct a Triangle Given the Lengths of Two Sides and the Bisector of Their Common Angle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

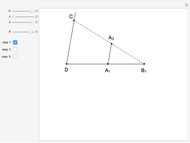
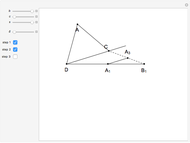
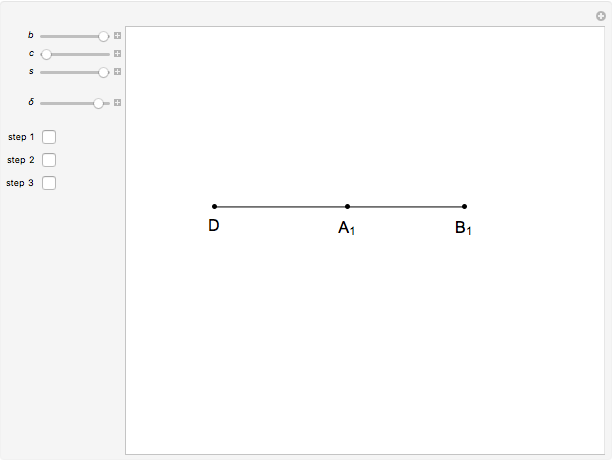
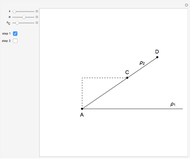
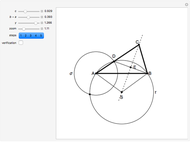
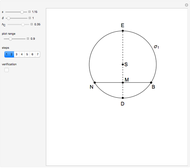
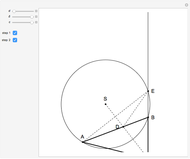
This Demonstration shows an alternative construction of a triangle 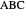given the lengths of the sides and and the length of the angle bisector of .

[more]

Construction

Draw the line segment with interior point so that and .

Step 1: Draw parallel lines through and at an arbitrary angle . On the line through , measure out so that . Let be the intersection of and the parallel line through .

Step 2: Construct an isosceles triangle with base and a leg of length .

Step 3: Let be a point such that and . That is, is a parallelogram. Let point be the intersection of the lines and .

Verification

In the triangle , divides in the ratio . So is the bisector of the angle at .

[less]

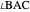Contributed by: Izidor Hafner (September 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] D. S. Modic, Triangles, Constructions, Algebraic Solutions (in Slovenian), Ljubljana: Math Publishers, 2009 pp. 44.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send