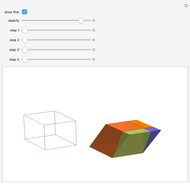
14-Piece Dissection of Juel's Pyramid into a Parallelepiped

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
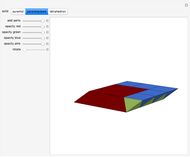
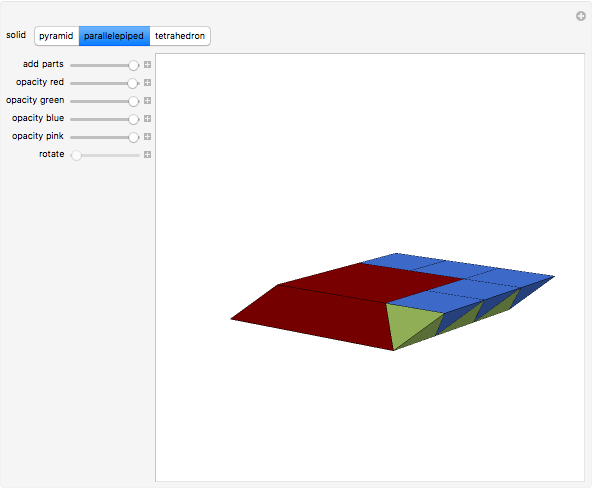
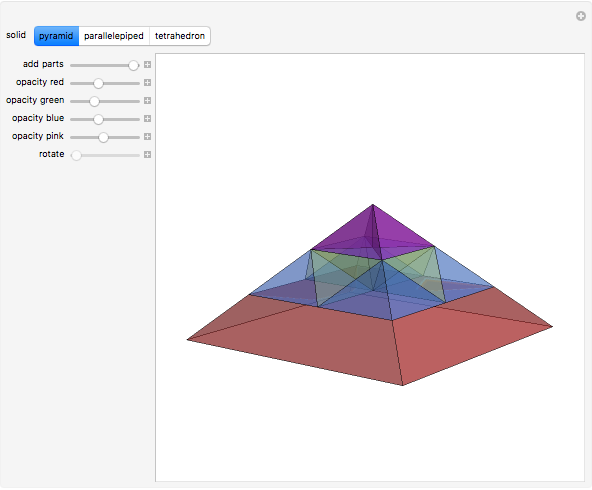
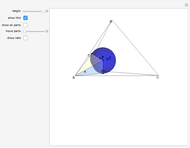
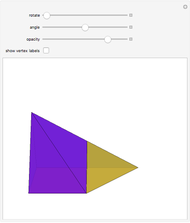
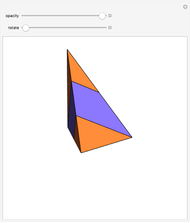
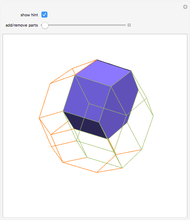
This Demonstration gives a 14-piece dissection of Juel's pyramid into a parallelepiped.
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The base of Juel's pyramid is a cube and its apex is the center of the cube. A dissection of the pyramid into a parallelepiped is described in [2]. The construction consists of cutting the pyramid into three layers. There is a hinged dissection of the Hill tetrahedron into a triangular prism, using a construction found independently by P. Schobi and A. Hanegraaf [1]. This is a three-piece dissection. Together these yield a four-piece dissection of Juel's pyramid into the prism. [1] G. N. Frederickson, Dissections: Plane & Fancy, New York: Cambridge University Press, 2002 p. 235. [2] H. Meschkowski, Grundlagen der Euklidischen Geometrie (Croatian edition), Zagreb: Skolska Knjiga, 1978 pp. 211–214.
Permanent Citation
"14-Piece Dissection of Juel's Pyramid into a Parallelepiped"
http://demonstrations.wolfram.com/14PieceDissectionOfJuelsPyramidIntoAParallelepiped/
Wolfram Demonstrations Project
Published: March 7 2011