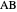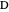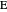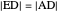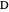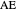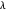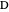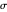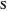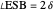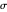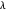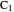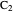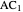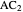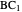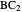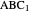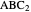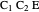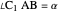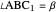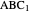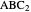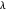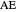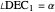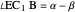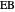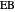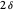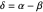1. Construct a Triangle Given the Length of the Base, the Difference of the Base Angles and the Foot of the Altitude to the Base
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
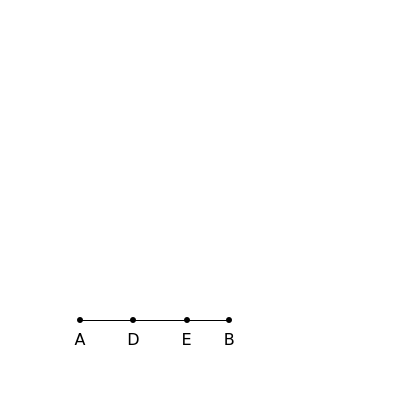
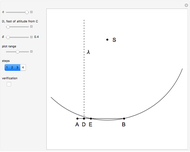
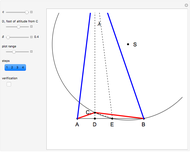
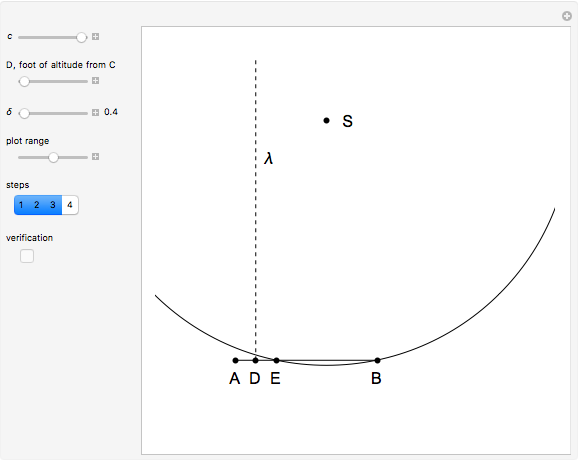
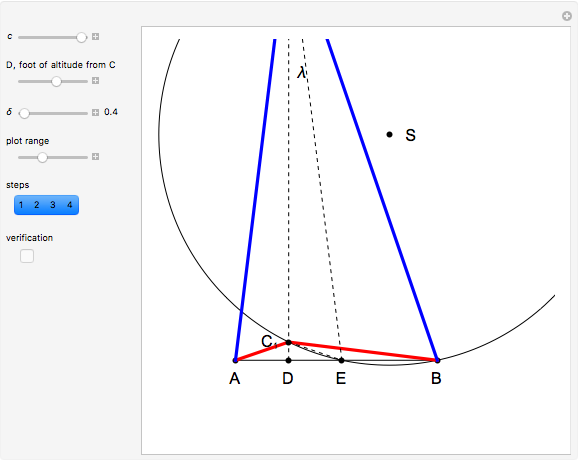
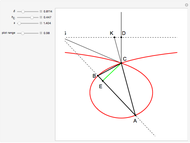
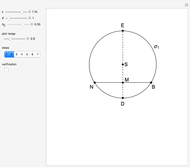
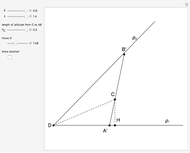
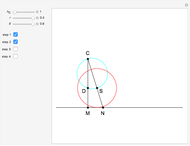
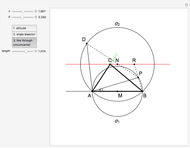
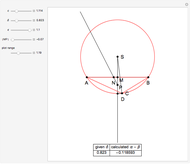
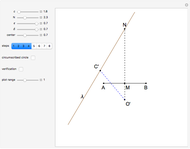
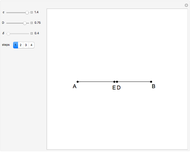
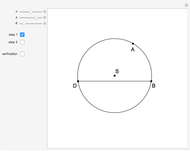
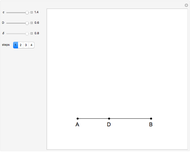
This Demonstration constructs a triangle given the length 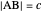 of its base, the difference
of its base, the difference  of the base angles and the foot
of the base angles and the foot 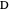 of the altitude from
of the altitude from 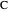 to the base.
to the base.
Contributed by: Izidor Hafner (August 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation