1D and 2D Singular Wavefronts

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
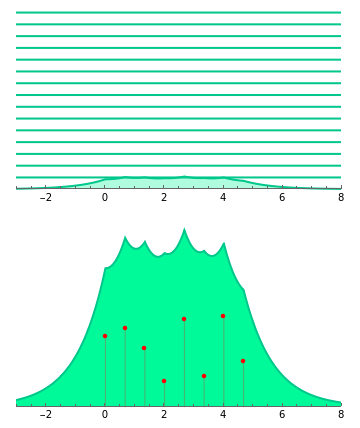
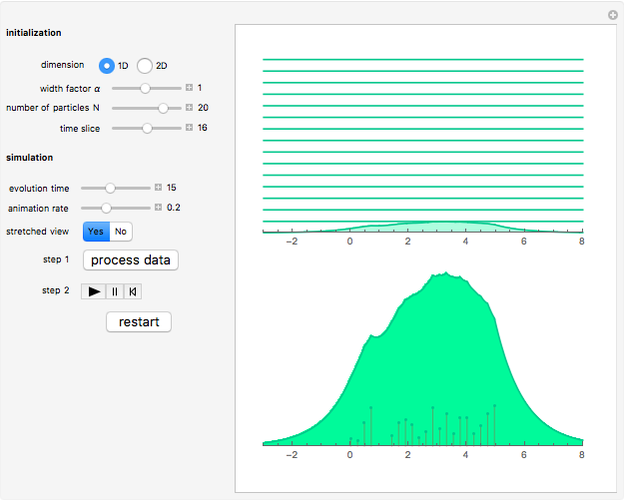
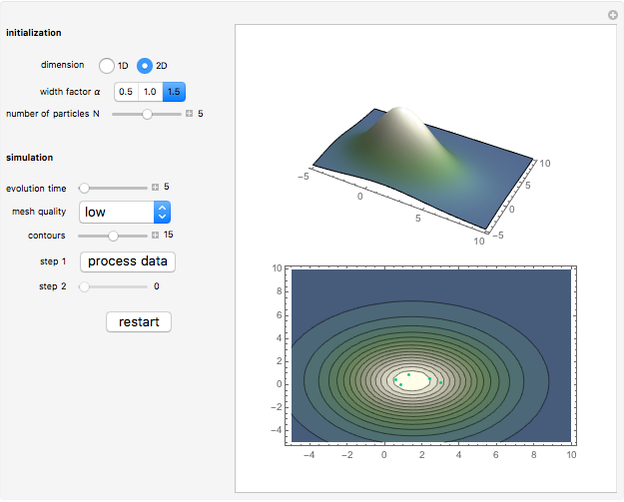
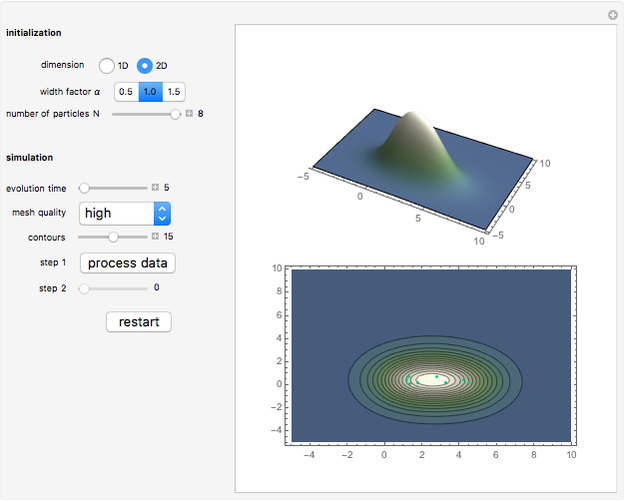
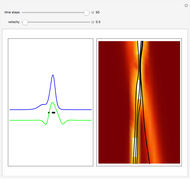
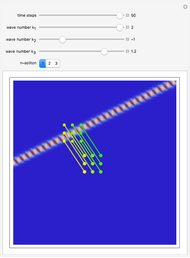
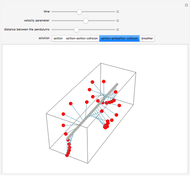
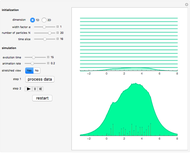
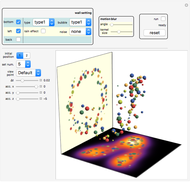
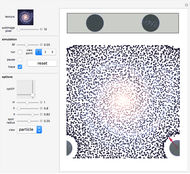
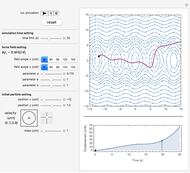
This Demonstration approximates the evolution of the velocity field of 1D and 2D singular wavefronts. The dynamics are fairly well governed by the weak solutions of the Euler–Poincaré differential equation. We use a particle method to solve the equation; all the particles (red points) are initially distributed at random within some area. The data was prepared offline in advance for efficiency. In the 2D case, points have different color opacities according to their individual weights.
Contributed by: Yiyang Li (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Introduction
As one of the most impressive nonlinear internal wave trains so far observed, the transbasin oceanic internal waves [photo link], which propagate for many hundreds of kilometers across basins and interact with one another, can be described by the weak solutions [1] of the Euler–Poincaré differential equation (EPDiff equation) on the diffeomorphism group of 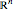 , or of an
, or of an  -dimensional manifold
-dimensional manifold 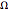 . In the case of one spatial dimension, the EPDiff equation can be derived from the Camassa–Holm (CH) shallow water wave equation [
. In the case of one spatial dimension, the EPDiff equation can be derived from the Camassa–Holm (CH) shallow water wave equation [ , 3], which has "peakon" solutions and possesses one order of accuracy in the asymptotic expansion beyond the Korteweg–de Vries (KdV) equation [4], which has "soliton" solutions that interact by the exchange of momentum in unidirectional elastic collisions. However, as pointed out in [5], "EPDiff" distinguishes "CH" because the Euler–Poincaré (EP) equations describe geodesic motion with respect to any metric that defines a norm on the vector space of the Lie algebra of a Lie group, whereas CH only refers to the shallow water wave equations for the case of one spatial dimension. For the purpose of a mathematically as well as historically concise perspective of the role played by the EPDiff equation when it comes to numerical singular wavefront simulation, the papers [6,
, 3], which has "peakon" solutions and possesses one order of accuracy in the asymptotic expansion beyond the Korteweg–de Vries (KdV) equation [4], which has "soliton" solutions that interact by the exchange of momentum in unidirectional elastic collisions. However, as pointed out in [5], "EPDiff" distinguishes "CH" because the Euler–Poincaré (EP) equations describe geodesic motion with respect to any metric that defines a norm on the vector space of the Lie algebra of a Lie group, whereas CH only refers to the shallow water wave equations for the case of one spatial dimension. For the purpose of a mathematically as well as historically concise perspective of the role played by the EPDiff equation when it comes to numerical singular wavefront simulation, the papers [6,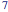 ] and the references therein are recommended.
] and the references therein are recommended.
Using vector notation, the EPDiff equation in the  -dimensional case on
-dimensional case on 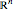 reads
reads
(1) 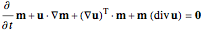 ,
,
(2) 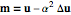 ,
,
with positive length scale factor  . By using the Einstein summation convention and writing
. By using the Einstein summation convention and writing
(3) 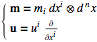
which regards  as a one-form density and
as a one-form density and  as a vector field, the EPDiff equation becomes
as a vector field, the EPDiff equation becomes
(4) 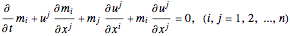 .
.
It can be solved with a particle approximation method [1], which yields solitary wave structures. The (approximate) weak solution of Eq. (1) and Eq. (2) can be expressed as
(5) 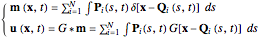
with
(6) 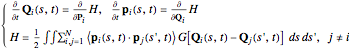
As to Eq. (5),  is the total number of particles,
is the total number of particles, 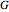 is a Green's function for the Helmholtz operator and can take many forms [
is a Green's function for the Helmholtz operator and can take many forms [ ], the symbol
], the symbol  denotes convolution and
denotes convolution and  for
for  . The solutions
. The solutions 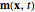 are vector-valued functions supported in
are vector-valued functions supported in 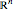 on a set of
on a set of  surfaces or curves of codimension
surfaces or curves of codimension  with
with 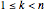 , and
, and 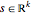 . When evaluated along the curve
. When evaluated along the curve  , it can be proved that
, it can be proved that
(7) 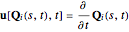 ,
,
which means  (or more specifically,
(or more specifically, 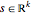 ) are equivalent to the Lagrangian coordinates. The solution
) are equivalent to the Lagrangian coordinates. The solution 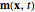 is the momentum map for singular solutions of the EPDiff equation.
is the momentum map for singular solutions of the EPDiff equation.
As to Eq. (6), the symbol 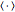 denotes the inner product,
denotes the inner product, 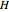 is the Hamiltonian function, and the sets
is the Hamiltonian function, and the sets 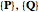 satisfy canonical Hamiltonian dynamics.
satisfy canonical Hamiltonian dynamics.
Incidentally, if we use 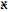 to denote the Lie algebra of vector fields on an
to denote the Lie algebra of vector fields on an  -dimensional manifold
-dimensional manifold 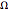 , let
, let 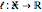 be a given Lagrangian and let
be a given Lagrangian and let 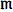 denote the space of one-form (momentum) densities on
denote the space of one-form (momentum) densities on 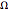 , then the EPDiff equation can be concisely written as [6]
, then the EPDiff equation can be concisely written as [6]
(8) 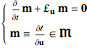
where 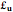 denotes the Lie derivative of momentum
denotes the Lie derivative of momentum  with respect to velocity
with respect to velocity  , and
, and  is defined as the functional derivative of the Lagrangian
is defined as the functional derivative of the Lagrangian  with respect to fluid velocity
with respect to fluid velocity 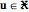 .
.
1D simulation
If we denote partial derivatives as subscripts, then in the case  Eq. (4) and Eq. (2) become
Eq. (4) and Eq. (2) become
(9) 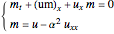
Adopting a particle method [1], its approximate numerical solution takes the form of a linear combination of Dirac distributions
(10) 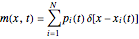 ,
,
where  represents the location of particle
represents the location of particle 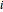 and
and 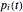 the corresponding weight at time
the corresponding weight at time  . The evolution of
. The evolution of  and
and 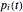 obey the equations
obey the equations
(11) 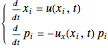
with  . If we take Green's function
. If we take Green's function 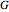 as
as
(12) 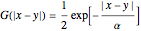 ,
,
then from the particle method we have [9]
(13) 
By solving Eqs. (10), (11), and (13) we can obtain 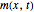 and
and 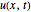 . In this Demonstration we show only the evolution of the velocity field
. In this Demonstration we show only the evolution of the velocity field 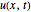 .
.
2D simulation
In the case  , Eq. (4) and Eq. (2) become
, Eq. (4) and Eq. (2) become
(14) 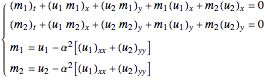
where  ,
, 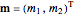 , and
, and 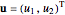 . Adopting the particle method [1], its approximate numerical solution also takes the form of a linear combination of Dirac distributions
. Adopting the particle method [1], its approximate numerical solution also takes the form of a linear combination of Dirac distributions
(15) 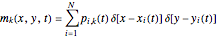 ,
, 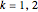
where 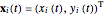 represents the location of particle
represents the location of particle 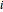 and
and 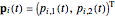 the corresponding weights at time
the corresponding weights at time  . The evolution of
. The evolution of  and
and 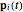 obey the following equations
obey the following equations
(16) 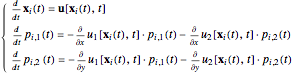
On the other hand, from the particle method we have [9]
(17) 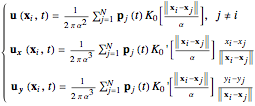
where 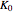 is the modified Bessel function (which serves as a Green's function) and
is the modified Bessel function (which serves as a Green's function) and  is its derivative. Considering that
is its derivative. Considering that 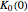 is a singularity, it can be predicted that Eq. (17) may yield relatively very high values if two particles approach each other. So it is necessary to regularize the solution values at each step. To do this, a cutoff function
is a singularity, it can be predicted that Eq. (17) may yield relatively very high values if two particles approach each other. So it is necessary to regularize the solution values at each step. To do this, a cutoff function 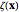 is usually adopted, which is taken as a smooth approximation of the Dirac delta function and thus satisfies
is usually adopted, which is taken as a smooth approximation of the Dirac delta function and thus satisfies
(18) 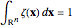 .
.
In practice, a further modified function  is often used, which is defined as
is often used, which is defined as
(19) 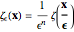 .
.
This allows replacing 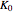 with its modification
with its modification  , with which the solutions can be regularized as
, with which the solutions can be regularized as
(20) 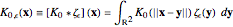 ,
,
where  again denotes convolution. The Gaussian function, which is regarded as one of the simplest examples of a cutoff function, is used here,
again denotes convolution. The Gaussian function, which is regarded as one of the simplest examples of a cutoff function, is used here,
(21) 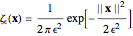 ,
,
so the modification  in our case is determined as [9]
in our case is determined as [9]
(22) 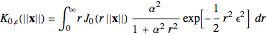 ,
,
where 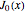 is the Bessel function of the first kind. By solving Eqs. (15), (16), and (17) and replacing
is the Bessel function of the first kind. By solving Eqs. (15), (16), and (17) and replacing 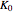 with
with  in Eq. (17), we can obtain
in Eq. (17), we can obtain 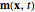 and
and  . As
. As  and its derivative
and its derivative 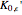 are numerically difficult to calculate (considering the property of
are numerically difficult to calculate (considering the property of 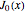 and the infinite integral limit), we use their approximate interpolation function instead, which was directly copied in the initialization code to shorten the processing time. Again, we show only the evolution of the velocity field
and the infinite integral limit), we use their approximate interpolation function instead, which was directly copied in the initialization code to shorten the processing time. Again, we show only the evolution of the velocity field  here.
here.
Provided that at least several hundred particles are used in this case, the EPDiff equation can yield very nice results representing the motion of internal wave trains. But as a real-time simulation, the upper limit of the particle number cannot be set that high as it would take too long to calculate, so up to eight particles can be initially distributed in this Demonstration.
Note 1
The "process data" function was tested on a computer with an Intel core i7 860 processor and sufficient DDR3 1333MHz memory. It will take only several seconds (from less than 0.001s with the minimum settings up to about 6s with the maximum settings) to complete in the 1D case. However, in the 2D case, it will take about 0.5–1s, 2–3s, and 60–80s for the minimum, default, and maximum settings, respectively.
Note 2 (optional)
Depending on the speed of the computer, the simulation may not run smoothly when the number of particles is large. We offer the option of exporting animations to video, which can provide much smoother animations and a better understanding of the dynamics at the cost of a longer export time. In order to do this, remove the comments from three code segments in the source code and then rerun the program (you must use Mathematica not CDF Player):
1. In the main code part, (* Export to video *),
2. In the “Visible Controls” part, (* The control of video export *),
3. In the TrackedSymbols:>{} part, uncomment (*,toVideo*).
The frame rate is set as 20 frames/second for both the 1D and 2D cases. The video files will be named as either "peakons1D.avi" or "peakons2D.avi" and will be saved in the directory containing this source code file (any older file with the same name will be replaced). Based on our tests, with the default settings and on the same computer, it will take about 3 minutes and 5–6 minutes for the export process to complete the 1D and 2D cases, respectively, and the sizes of the corresponding video files will be 135.21MB and 45.37MB. Increasing the number of particles or the mesh quality in the 2D case may greatly increase the export time. After the video file is exported, your system will automatically open it using the default application. If the video cannot be played smoothly, you can manually open it with another player installed on your computer.
Further reading
More details, including several nice 2D and 3D evolution videos, can also be accessed on Martin Staley's personal page, http://math.lanl.gov/~staley/.
References
[1] P. A. Raviart, "An Analysis of Particle Methods, Numerical Methods in Fluid Dynamics, in Lecture Notes in Mathematics, Vol. 1127, Berlin: Springer, 1985 pp. 243–324.
[2] R. Camassa and D. D. Holm, "An Integrable Shallow Water Equation with Peaked Solitons," Physical Review Letters, 71(11), 1993 pp. 1661–1664.
[3] R. Camassa, D. D. Holm, and J. M. Hyman, "A New Integrable Shallow Water Equation," Advances in Applied Mechanics, 31, 1994 pp. 1–33.
[4] E. M. de Jager, "On the Origin of the Korteweg–de Vries Equation," arXiv:math/0602661v1, 2006.
[5] C. J. Cotter and D. D. Holm, "Discrete Momentum Maps for Lattice EPDiff," arXiv:math/0602296, 2006.
[6] D. D. Holm and J. E. Marsden, "Momentum Maps and Measure-Valued Solutions (Peakons, Filaments, and Sheets) for the EPDiff Equation," Progress in Mathematics, 232, 2005 pp. 203–235.
[7] D. D. Holm and R. I. Ivanov, "Smooth and Peaked Solitons of the CH Equation," Journal of Physics A: Mathematical and Theoretical, 43(43), 2010 pp. 434003 (18pp).
[8] O. B. Fringer and D. D. Holm, "Integrable vs. Nonintegrable Geodesic Soliton Behavior," Physica D: Nonlinear Phenomena, 150(3–4), 2001 pp. 237–263.
[9] A. Chertock, J. Marsden, and P.D. Toit, "Integration of the EPDiff Equation by Particle Methods," submitted (Mar 17, 2011) http://www4.ncsu.edu/~acherto/papers/ChDTuMa.pdf.
Permanent Citation