1D Heat Conduction through Biological Tissue

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
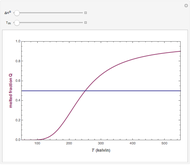
This Demonstration is about time-varying heat conduction in biological tissue. The main objective of a conduction analysis is to determine temperature distribution in a tissue medium, that is, to know the temperature in the tissue as a function of space at the steady state and as a function of time during the transient state. Once this temperature distribution is known, the heat flux at any point within or on the surface the tissue may be computed from Fourier's law. A knowledge of the temperature distribution within a tissue can be used in medical applications via a determination of the thermal stresses and distortion. The optimization of the thickness of a tissue can be studied by knowing the temperature distribution and the appropriate heat transfer characteristics, which indicate the appropriate temperature distribution at every point within the tissue categorized into the quasi-conductor medium at 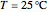 .
.
Contributed by: Muhamad Hamdi and Yusof Munajat (May 2013)
Biophysics Department, University of Riau, Indonesia and Physics Department, University of Technology Malaysia, Johor Bahru
Open content licensed under CC BY-NC-SA
Snapshots
Details
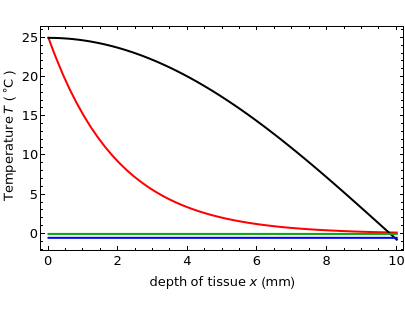
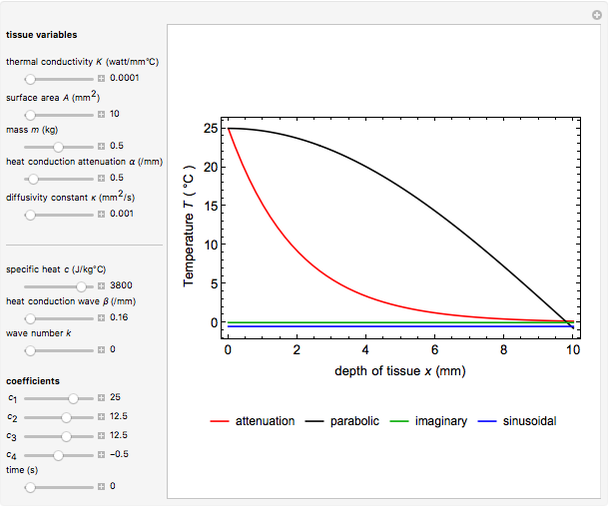
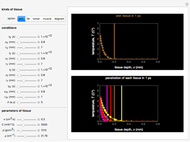
Snapshot 1: Parabolic equations typically describe propagation problems. Time usually appears only in a first derivative, and the process involves only the forward direction of  . The graph shows that type of the parabolic solution set with a value of heat conduction wave constant
. The graph shows that type of the parabolic solution set with a value of heat conduction wave constant 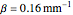 for the complex exponential solution (the maximum real part is in black and the minimum imaginary part is in green; see legend). On the other hand, the attenuation solution of the thermal gradient equation (red) is adjusted at a value of heat conduction attenuation constant
for the complex exponential solution (the maximum real part is in black and the minimum imaginary part is in green; see legend). On the other hand, the attenuation solution of the thermal gradient equation (red) is adjusted at a value of heat conduction attenuation constant 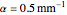 in tumor tissue. There is also the heat conduction wave sinusoidal solution form (blue) but no parabolic solution type. The initial condition prescribes the unknown function
in tumor tissue. There is also the heat conduction wave sinusoidal solution form (blue) but no parabolic solution type. The initial condition prescribes the unknown function 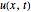 throughout the given region at some initial time
throughout the given region at some initial time  , in this case
, in this case  . Mathematically speaking, the time and the space coordinates are regarded as independent variables. In this respect, the initial condition is merely a point prescribed on the
. Mathematically speaking, the time and the space coordinates are regarded as independent variables. In this respect, the initial condition is merely a point prescribed on the  axis and the boundary conditions are prescribed in this case as two points on the
axis and the boundary conditions are prescribed in this case as two points on the  axis. Initial conditions are usually prescribed at a variable time
axis. Initial conditions are usually prescribed at a variable time  or
or  , but time dependence need not be considered.
, but time dependence need not be considered.
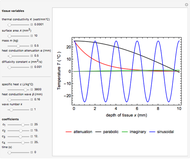
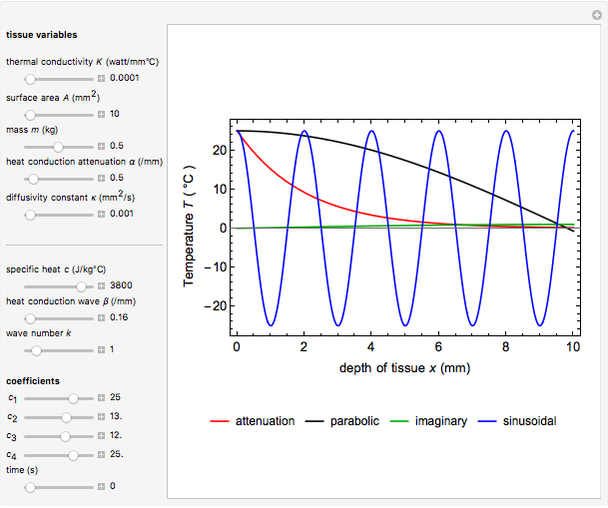
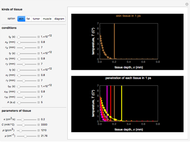
Snapshot 2: Unlike the parabolic solution (black and red), the heat conduction wave solution (blue) does not decay with depth  and time
and time  . Instead, there are standing waves set up between the two sides of the medium boundary. With amplitude constant
. Instead, there are standing waves set up between the two sides of the medium boundary. With amplitude constant  , the fundamental standing mode (
, the fundamental standing mode (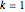 )
) 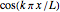 oscillates with a frequency
oscillates with a frequency 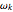 and with the
and with the 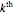 standing mode. An interesting interpretation of the graph shows that intersections of heat conduction wave propagation (blue) and parabolic heat conduction distribution (black and red) describe information from the tumor tissue temperature at discrete points only for heat propagation. It can be seen that temperature reduces the attenuation for the solution of the temperature gradient equation (red).
standing mode. An interesting interpretation of the graph shows that intersections of heat conduction wave propagation (blue) and parabolic heat conduction distribution (black and red) describe information from the tumor tissue temperature at discrete points only for heat propagation. It can be seen that temperature reduces the attenuation for the solution of the temperature gradient equation (red).
Snapshot 3: For the solution of temperature gradient equation at an internal line of symmetry, we need two boundary conditions in the  direction and one time condition. Boundary conditions are, as the name implies, frequently specified along the physical extremities of the tissue body; they can, however, also be internal—for example, a known temperature gradient at an internal line of symmetry. The time condition is usually the known initial temperature. As time increases from
direction and one time condition. Boundary conditions are, as the name implies, frequently specified along the physical extremities of the tissue body; they can, however, also be internal—for example, a known temperature gradient at an internal line of symmetry. The time condition is usually the known initial temperature. As time increases from  to
to 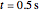 , the temperature reduces with increasing depth of tissue
, the temperature reduces with increasing depth of tissue  (red). This means that the temperature of the complex exponential (black) and sinusoidal (blue) solution is independent of time. The main mechanism for heat flow inside a tissue is through conduction, meaning that the gradient in the temperature within the tissue itself drives the flow.
(red). This means that the temperature of the complex exponential (black) and sinusoidal (blue) solution is independent of time. The main mechanism for heat flow inside a tissue is through conduction, meaning that the gradient in the temperature within the tissue itself drives the flow.
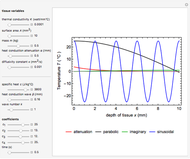
Snapshot 4: Heat conduction equation parabolic solution in the complex exponential form (black) can be set to be the same as the heat conduction wave pattern (blue) with its value of heat conduction wave 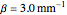 and each amplitude constant
and each amplitude constant 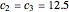 . Meanwhile, the solution of the temperature gradient equation reduces toward zero at
. Meanwhile, the solution of the temperature gradient equation reduces toward zero at 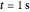 (red).
(red).
The description of conductive heat transfer rate at a point within tissue is related to the local temperature gradient by Fourier's law. We use the tumor tissue physical parameters to interpret its actual heat distribution or pattern for all boundary and initial conditions. There are Dirichlet conditions, where the value of the unknown 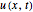 is specified at the spatial boundaries and Neumann conditions, with the values of the normal derivative of the unknown
is specified at the spatial boundaries and Neumann conditions, with the values of the normal derivative of the unknown 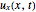 specified at the boundaries. They are the homogenous boundary conditions. In fact, at room temperature any medium has a lower temperature on the inside with no internal energy conversion used for the interpretation of heat conduction. We also analyze heat conduction to use the temperature gradient equation in the direction normal to the area. If the temperature changes with time, energy is either being stored in or removed from the medium. This indicates that the heat flow flux goes into or out of the medium. In principle, the thermal energy transfer resulting from the thermal gradient must be from a higher to a lower temperature. The consequence of energy conservation is that this storage rate is equal to the energy transfer rate within the medium, which can be calculated by
specified at the boundaries. They are the homogenous boundary conditions. In fact, at room temperature any medium has a lower temperature on the inside with no internal energy conversion used for the interpretation of heat conduction. We also analyze heat conduction to use the temperature gradient equation in the direction normal to the area. If the temperature changes with time, energy is either being stored in or removed from the medium. This indicates that the heat flow flux goes into or out of the medium. In principle, the thermal energy transfer resulting from the thermal gradient must be from a higher to a lower temperature. The consequence of energy conservation is that this storage rate is equal to the energy transfer rate within the medium, which can be calculated by
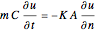 ,
,
where 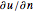 is the temperature gradient in the direction normal to the area
is the temperature gradient in the direction normal to the area  , mass
, mass  , specific heat
, specific heat  , and thermal conductivity
, and thermal conductivity 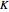 . The result is that the amount of thermal energy conducted through a medium is proportional to the cross-sectional area, the temperature difference, and the time interval. In many one-dimensional problems, we may write the temperature gradient simply by inspection of the physical situation, which requires an energy equation that governs the temperature distribution. Analysis of such transient problems can be undertaken with the 1D general conduction equation,
. The result is that the amount of thermal energy conducted through a medium is proportional to the cross-sectional area, the temperature difference, and the time interval. In many one-dimensional problems, we may write the temperature gradient simply by inspection of the physical situation, which requires an energy equation that governs the temperature distribution. Analysis of such transient problems can be undertaken with the 1D general conduction equation,
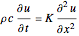 .
.
The useful combination of terms already considered is the thermal diffusivity  , where
, where  is density. Analytical solutions of the above equations using Mathematica are as follows for the thermal gradient,
is density. Analytical solutions of the above equations using Mathematica are as follows for the thermal gradient,
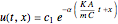 ,
,
and for the 1D conduction equation,
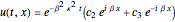 ,
,
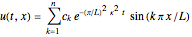 ,
,
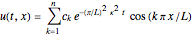 .
.
The partial differential equation of heat conduction in tissue medium with the boundary conditions tell us what is happening at the boundaries to affect the solution inside the domain of interest, whereas the initial conditions tell us the state from which the solution evolves. Without it, the mathematical specification of the problem is incomplete. Physically, we understand that two identical quasi-conductor media (e.g. biological tissues) with the same boundary conditions may evolve differently if they start with different initial temperatures. In this interpretation, the above solutions depend on the heat conduction main parameters such as a tissue heat conduction attenuation, heat conduction wave, and thermal diffusivity.
To better understand the heat conduction in tissue physical interpretation using the heat conduction equation, we need to look more in detail on the thermal properties of tissue. For physical problems, it is not sufficient to know that the problem exists and has a unique solution. Hence the continuity requirement is not only useful but also essential. If the solution is to have physical significance, a small change in the initial data must produce a small change in the solution. The data in a physical problem is normally obtained from an experiment, and is approximated in order to solve the problem by numerical or approximate methods. It is essential to know that the process of making an approximation to the data produces only a small change in the solution.
References
[1] H. Ilham, Introduction to Biophysics, 1st ed., Pekanbaru, Riau, Indonesia: RUEDC-Press, 2007.
[2] A. Tveito and R. Winther, Introduction to Partial Differential Equations: A Computational Approach, New York: Springer-Verlag, 1998.
Permanent Citation