Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

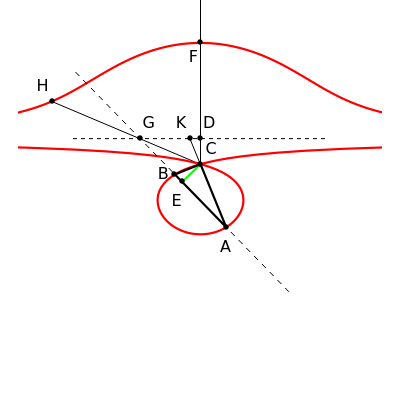
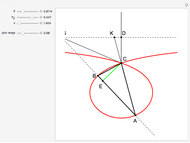
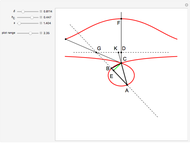
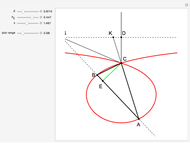
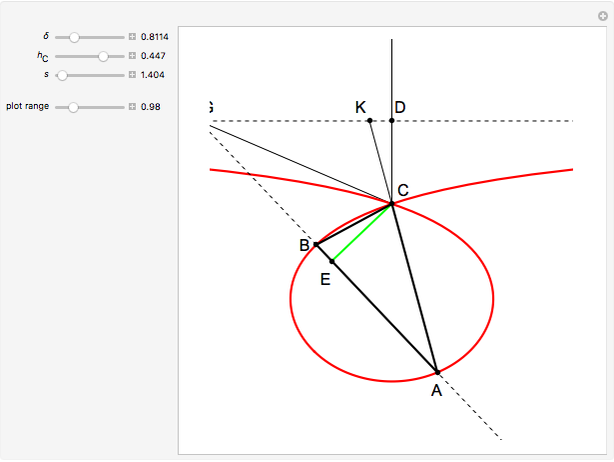
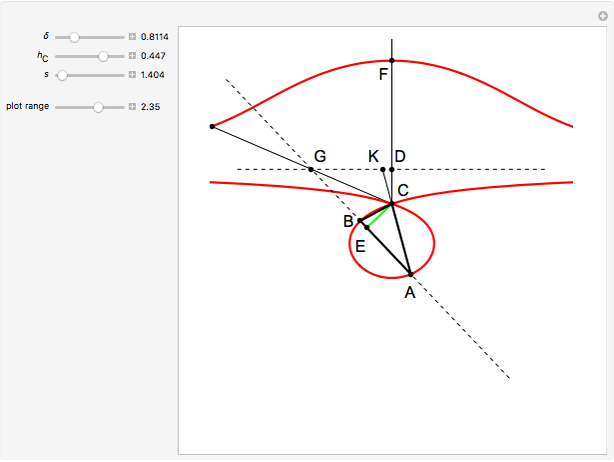
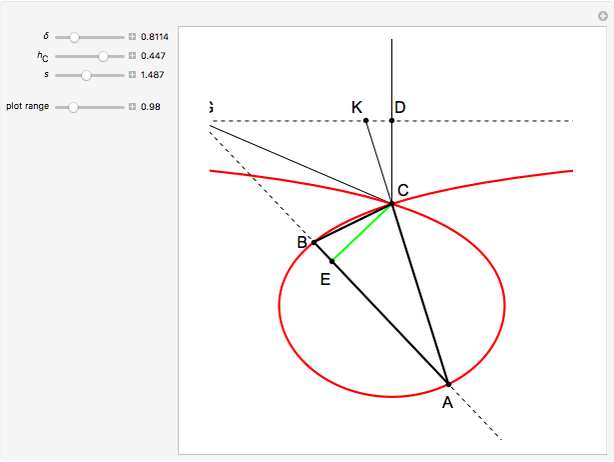
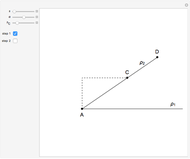
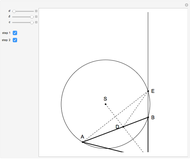
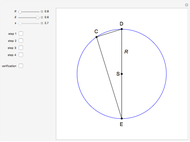
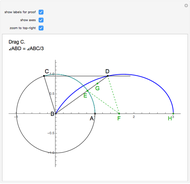
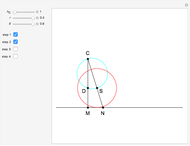
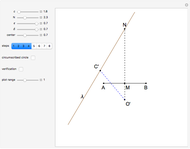
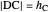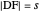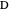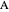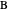24b. Construct a Triangle Given the Length of the Altitude to the Base, the Difference of Base Angles and the Sum of the Lengths of the Other Sides

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

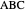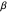This Demonstration uses a conchoid to construct a triangle given the difference of the base angles and 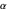, the length of the altitude 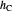from the base and the sum of the lengths of the legs.

[more]

The conchoid, shown in red, determined by and , intersects the straight line through that forms an angle with the horizontal line through in the points and . The triangle is the solution.

[less]

Contributed by: Nada Razpet, Marko Razpet and Izidor Hafner (October 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

While looking for different solutions to Plemelj's triangle construction problem (given the length of the base , the altitude 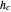and the difference 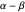), we came across a more difficult problem: instead of , 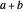is given. The problem was solved by Nada Razpet using the conchoid of Nicomedes.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send