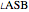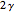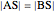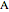Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

27a. Construct a Triangle Given a Side, the Length of the Altitude to It and the Opposite Angle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

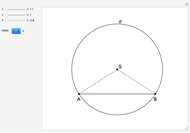
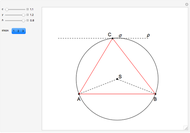
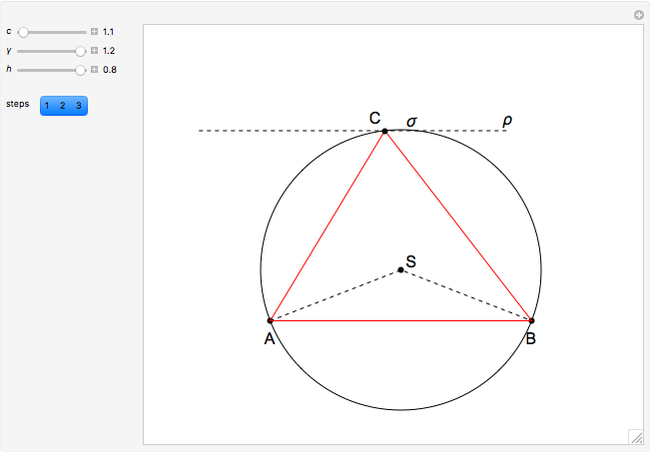
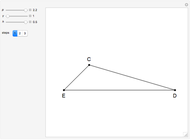
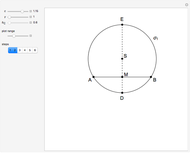
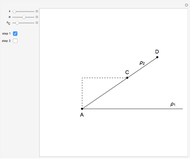
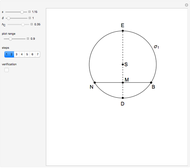
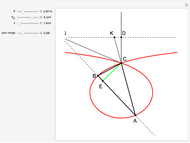
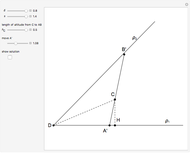
This Demonstration constructs a triangle given the length of the base 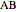, the angle at and the length of the altitude from to the base.

[more]

Construction

1. Draw a line segment of length .

2. Draw the point so that the angle equals and . Draw the circle with center through and .

3. Draw a line parallel to at distance . The third point of the triangle is the intersection of and .

Verification

The angle at is , since the central angle that subtends equals .

[less]

Contributed by: Izidor Hafner (October 2017)
Open content licensed under CC BY-NC-SA

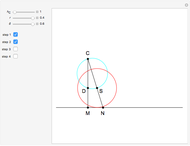
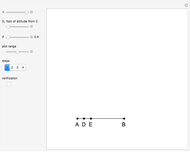
Snapshots

Details

This construction was taken from [1].

Reference

[1] G. Polya, How to Solve It: A New Aspect of Mathematical Method, 2nd ed., Princeton, NJ: Princeton University Press, 1957.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send