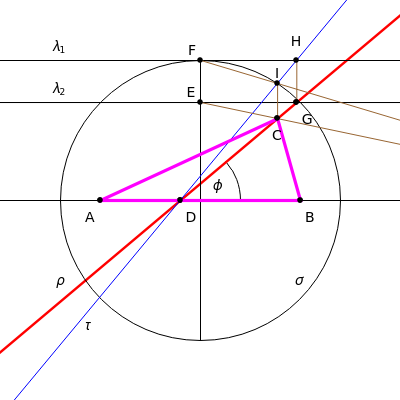
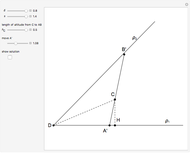
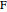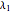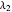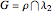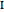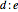28. Construct a Triangle ABC Given the Length of AB, the Sum of the Other Two Sides, and a Line Containing C
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
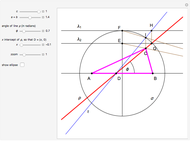
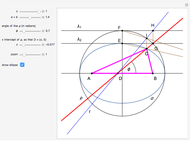
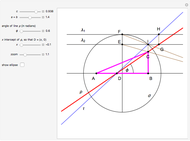
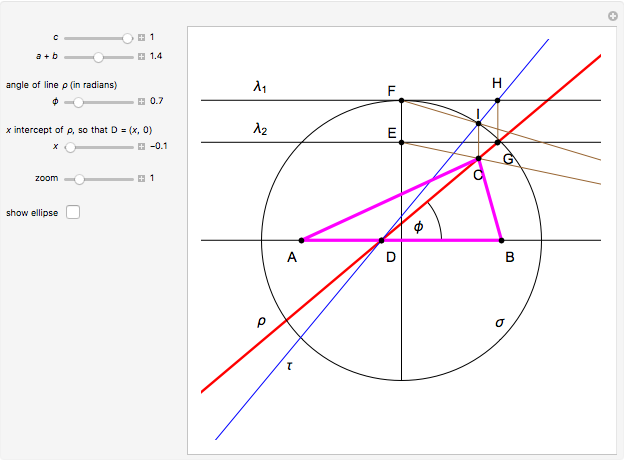
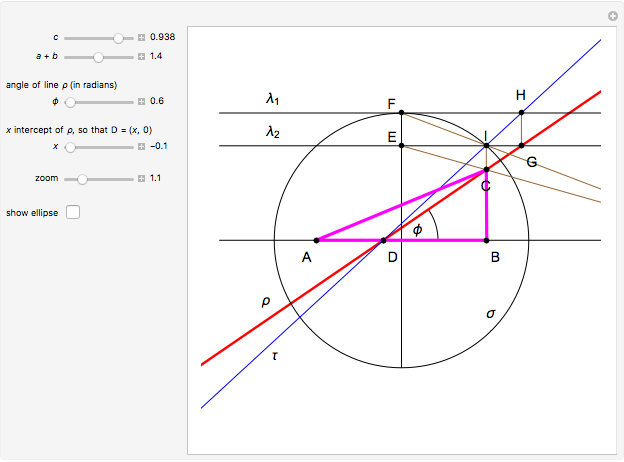
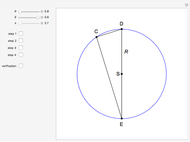
This Demonstration shows how to construct a triangle  given the length
given the length  of the side opposite the vertex
of the side opposite the vertex  , the sum of the lengths of the other two sides
, the sum of the lengths of the other two sides  and a line
and a line  containing the vertex
containing the vertex  . Since
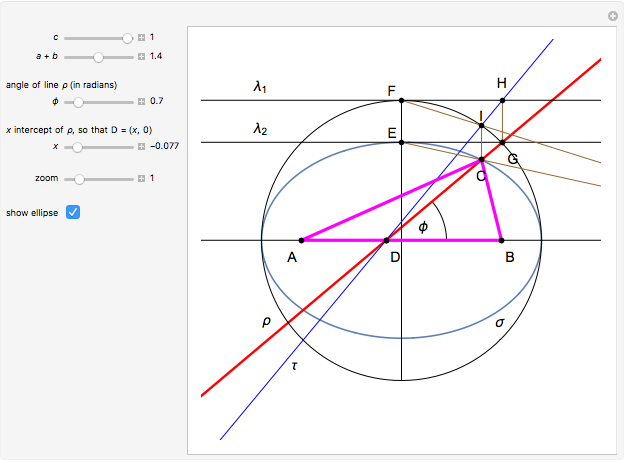
. Since  lies on the ellipse with foci
lies on the ellipse with foci 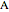 and
and 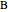 , the semi-axes of the ellipse are
, the semi-axes of the ellipse are  and
and 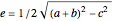 .
.
Contributed by: Marko Razpet and Izidor Hafner (March 2018)
Open content licensed under CC BY-NC-SA
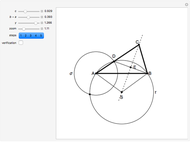
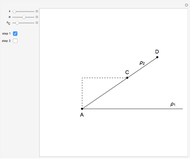
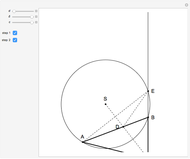
Snapshots
Details
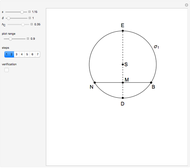
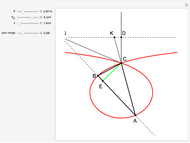
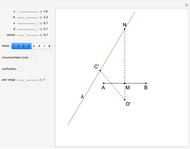
This construction is suggested by the linear transformation 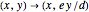 , which maps the ellipse
, which maps the ellipse 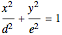 and the line
and the line 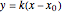 into the circle
into the circle 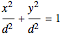 and the line
and the line 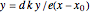 .
.
Permanent Citation