2-by-n Disk-Packing Paradox

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
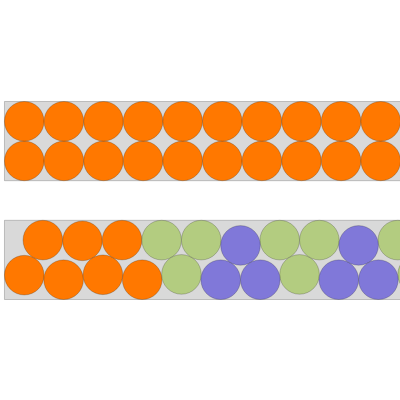
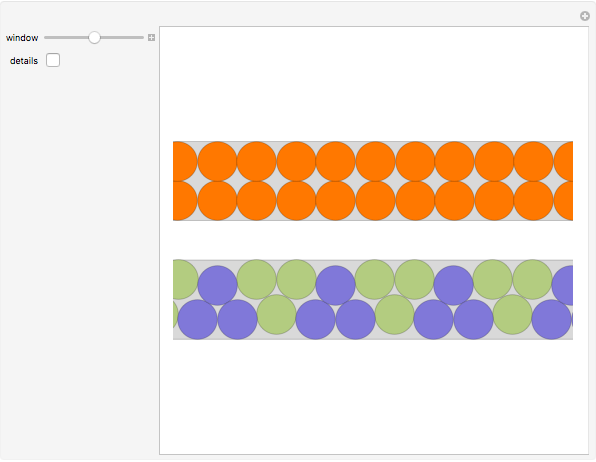
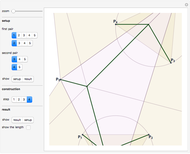
The top box shows that it is easy to place  unit diameter disks in a
unit diameter disks in a  rectangle, namely by fitting two disks at a time side by side.
rectangle, namely by fitting two disks at a time side by side.
Contributed by: Karl Scherer and Richard Hess (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The packing using triples of disks in the second box is more efficient:
While for every two additional disks the top arrangement needs 1 unit length more, the arrangement with sets of two triples in the second rectangle uses only 0.99399 unit length per two disks.
Controls:
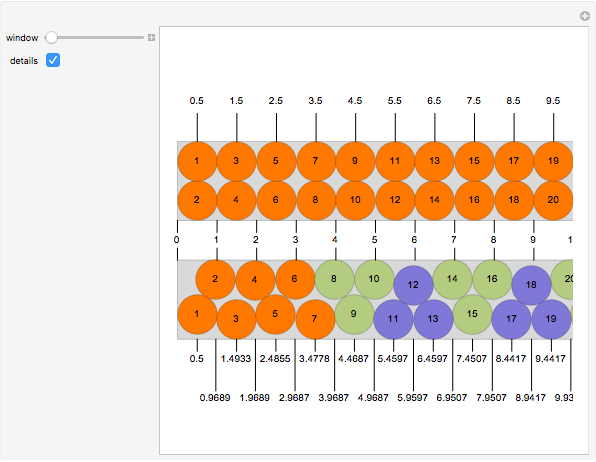
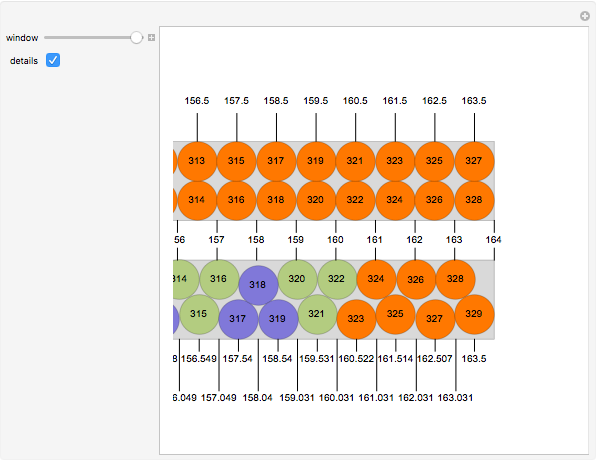
Use the "window" slider to view any part of the  rectangles.
rectangles.
Click the "details" button to display the  -coordinate of the centers of the disks and other information.
-coordinate of the centers of the disks and other information.
We suggest using the "window" slider only when the "details" option is switched off.
Construction of disk arrangement:
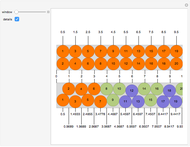
There are seven disks at each end and 105 sets of three disks in the middle. Start by placing the 105 triples into the center of the rectangle.
All disks that seem to touch in the diagram indeed touch each other, with the exception of disk 1 and disk 2, which do not touch each other. In detail:
Place 6 against the top and 8. Place 7 against 9 and the bottom. Place 5 next to 6 and 7. Place 4 against 5 and 6. Place 3 against the bottom and 5. Place 2 against 3 and 4 Place 1 against 2 and 3. Place reflections of all these to the right of the 105 center disks.
Permanent Citation