2D Quantum Problem: Particle in a Disk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
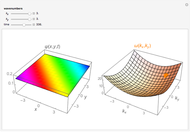
The wave functions of a quantum particle of mass 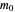 confined to a disk of radius
confined to a disk of radius 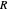 in the
in the 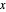 -
-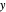 plane are derived. These functions
plane are derived. These functions 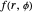 in polar coordinates are two-dimensional solutions of the Schrödinger equation with the potential
in polar coordinates are two-dimensional solutions of the Schrödinger equation with the potential  . There is an infinite number of functions
. There is an infinite number of functions 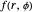 that fulfill the boundary condition
that fulfill the boundary condition  , depend on two independent integer quantum numbers
, depend on two independent integer quantum numbers 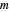 and
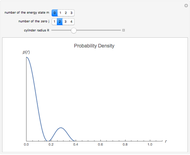
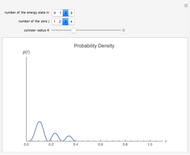
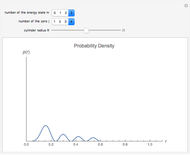
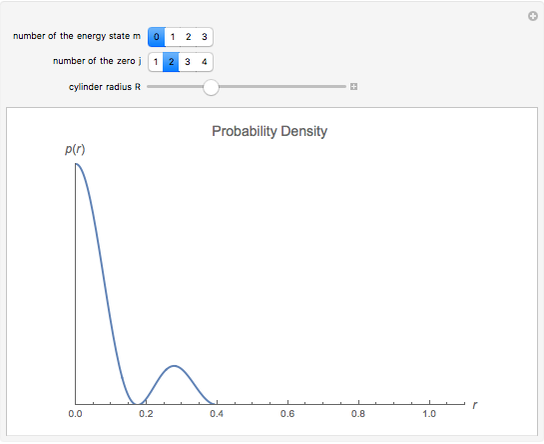
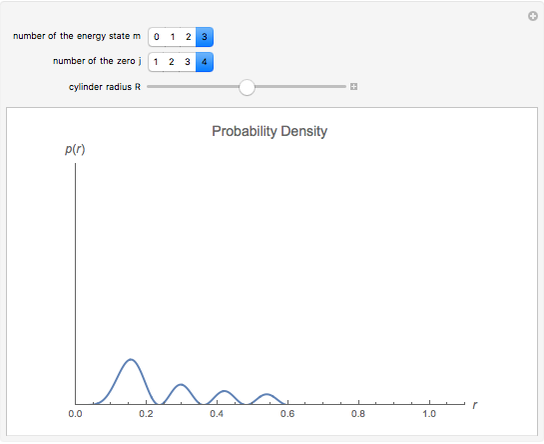
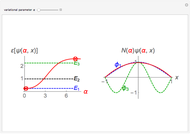
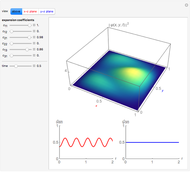
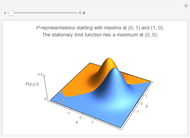
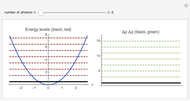
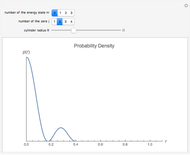
and 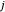 . This Demonstration shows the oscillating behavior of the (unnormalized) probability density
. This Demonstration shows the oscillating behavior of the (unnormalized) probability density 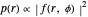 of a particle with different energy states inside the disk in the interval
of a particle with different energy states inside the disk in the interval 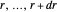 ,
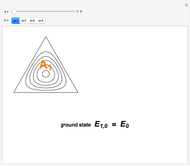
,  . The ground state is characterized by the quantum number
. The ground state is characterized by the quantum number 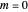 ; excited states have
; excited states have  .
.
Contributed by: Reinhard Tiebel (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The eigenvalue equation for the Hamiltonian 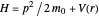 reads, in polar coordinates
reads, in polar coordinates  ,
,  :
: 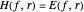 . In the quantum-mechanical position basis (
. In the quantum-mechanical position basis ( -representation), the momentum operator
-representation), the momentum operator 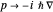 ("nabla" operator), so that the energy eigenvalue equation is transformed into a partial differential equation;
("nabla" operator), so that the energy eigenvalue equation is transformed into a partial differential equation;  is Planck's constant
is Planck's constant 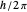 . The unique solutions regular at
. The unique solutions regular at 
 satisfying the boundary condition
satisfying the boundary condition 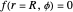 are Bessel functions
are Bessel functions 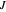 of integer order
of integer order 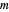 :
: 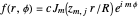 , where
, where 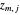 represent the
represent the 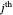 zero of the Bessel function
zero of the Bessel function 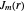 ,
, 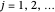 . The integers
. The integers 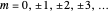 give the
give the  components of the angular momentum
components of the angular momentum 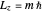 . The wave-mechanical probability densities
. The wave-mechanical probability densities 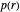 are oscillating functions and show analogous behavior to those of corresponding rectangular potential problems in one, two, and three dimensions, respectively.
are oscillating functions and show analogous behavior to those of corresponding rectangular potential problems in one, two, and three dimensions, respectively.
References
[1] J. J. Sakurai, Modern Quantum Mechanics, Reading, MA: Addison–Wesley Publishing Company, 1995.
[2] L. D. Landau and E. M. Lifschitz, Quantum Mechanics, Reading, MA: Addison-Wesley Publishing Company, 1958.
Permanent Citation