2x2 Ordinal Games

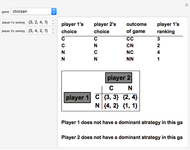
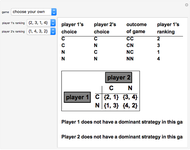
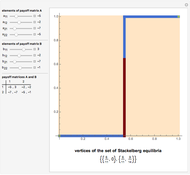
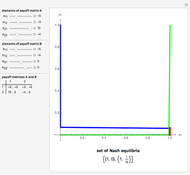
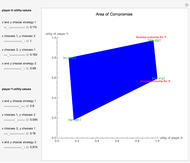
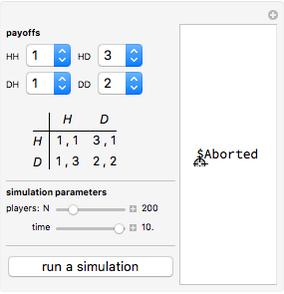
A 2×2 ordinal game consists of two players, each with the strategy options of cooperation or noncooperation with the other player (these options are denoted C and N, respectively, in this Demonstration). Each player then ranks the four possible resulting outcomes from four (most desirable for that player) down to 1 (least desirable). The game is summarized in a 2×2 matrix of ordered pairs, with the entries in each ordered pair being the rankings of the corresponding outcome by player 1 and player 2, respectively. A dominant strategy for a player is a strategy (a choice of C or N) with the property that such a choice results in a more favorable outcome for that player than the other choice would, regardless of the other player's choice of strategy. A Nash equilibrium is a choice of strategy by each player with the property that a unilateral change of strategy by either player is unfavorable to that player.