Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

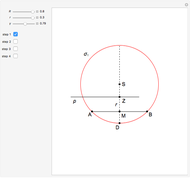
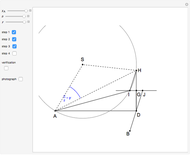
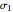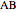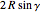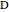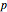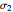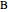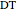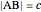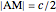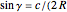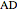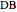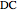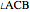4. Construct a Triangle Given Its Circumradius, Inradius and a Vertex Angle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

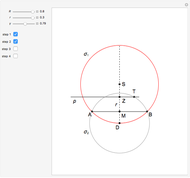
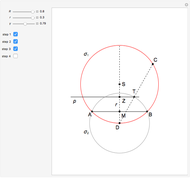
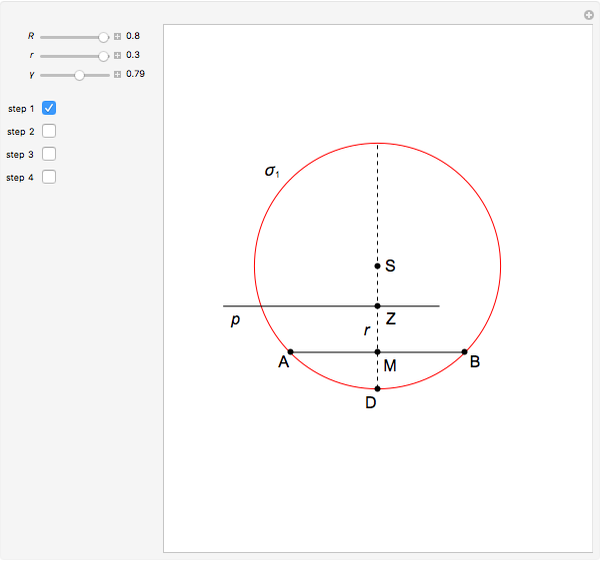
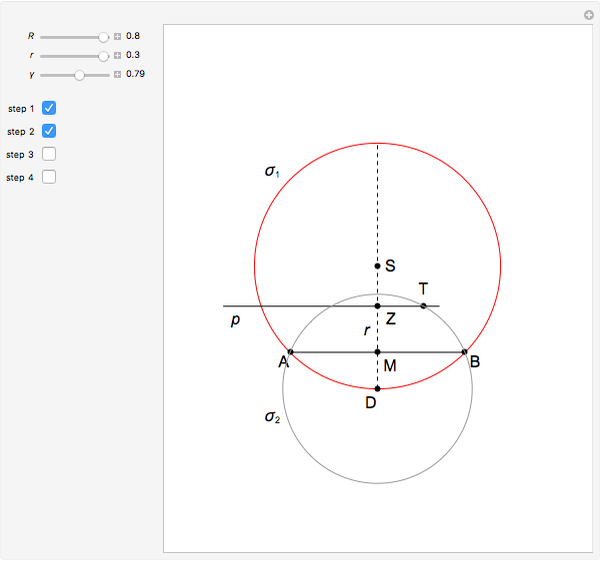
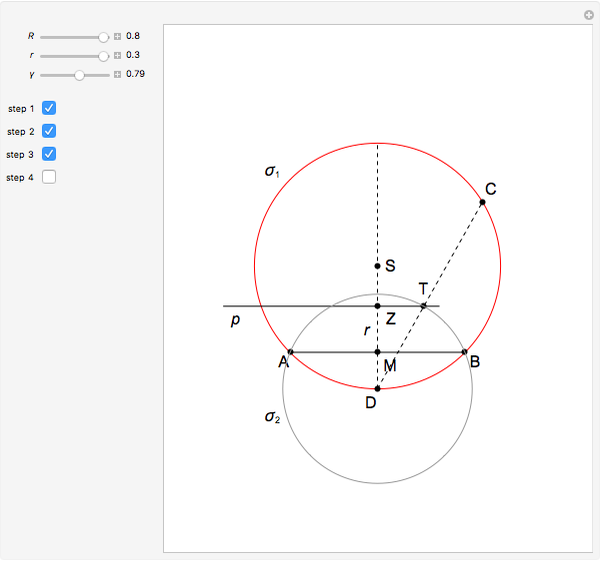
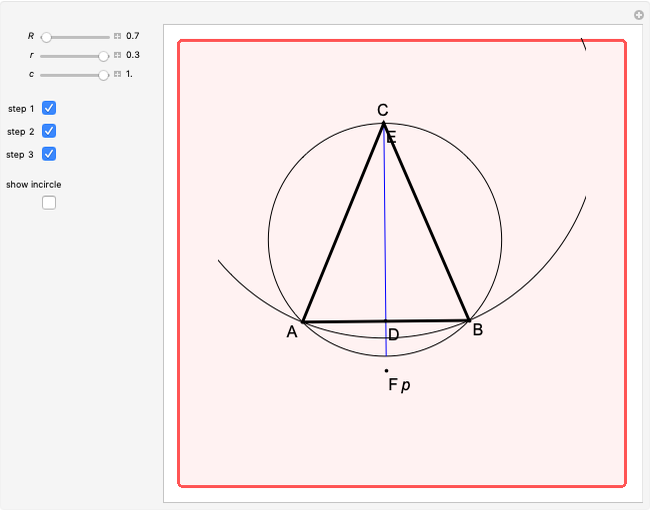
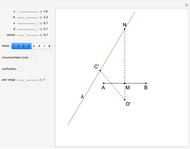
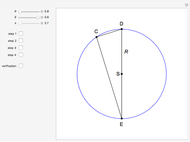
This Demonstration constructs a triangle 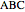given its circumradius 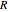, inradius and the angle at .

[more]

Construction

Draw a circle with center of radius and a chord of length . Let be the midpoint of and let be an endpoint of the diameter perpendicular to .

Step 1: Draw a line parallel to at distance from intersecting at .

Step 2: Draw a second circle with center through and . Let be one of the points of intersection of and .

Step 3: Let be the intersection of and .

Step 4: Draw the triangle and its incircle.

Verification

Theorem: Let . Then .

Proof: In the right-angled triangle , the hypotenuse length is and the leg , so ). Since the arc equals the arc , bisects . The distance of to is , so is the incenter of .

[less]

Contributed by: Izidor Hafner (August 2017)
Open content licensed under CC BY-NC-SA

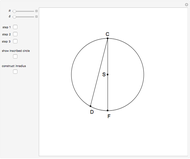
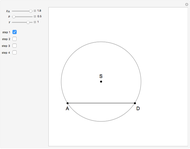
Snapshots

Details

Reference

[1] D. S. Modic, Triangles, Constructions, Algebraic Solutions (in Slovenian), Ljubljana: Math Publishers, 2009, p. 82.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send