54-Faced Space-Filling Polyhedron

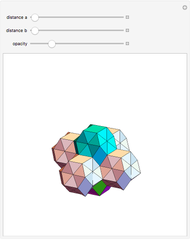
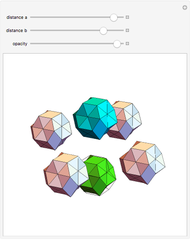
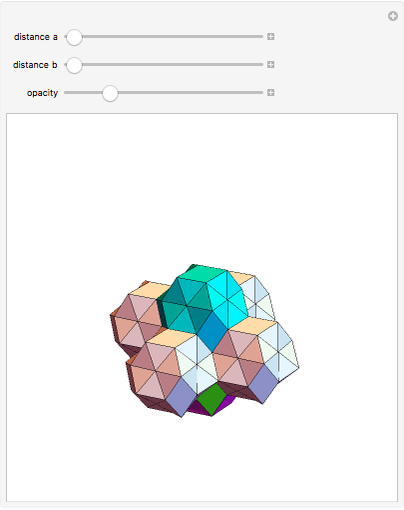
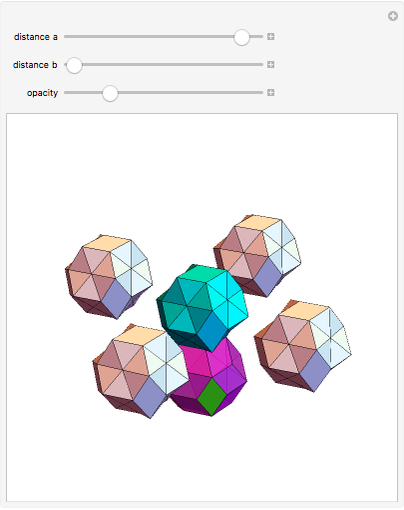
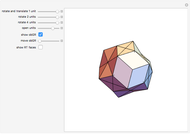
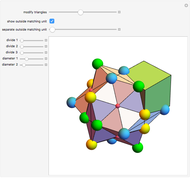
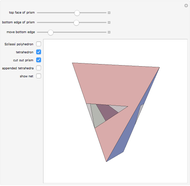
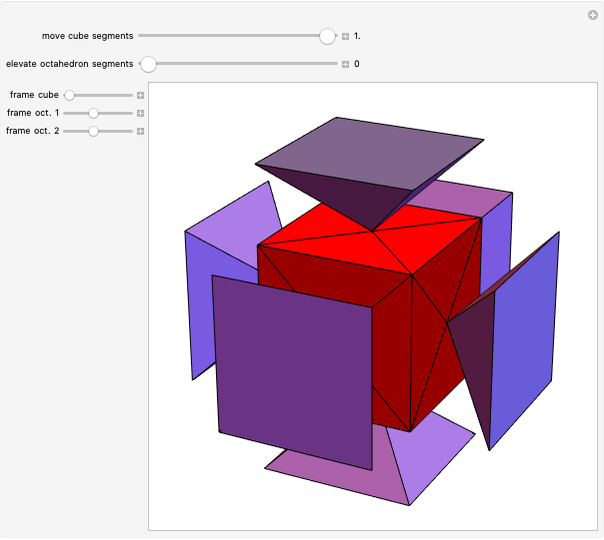
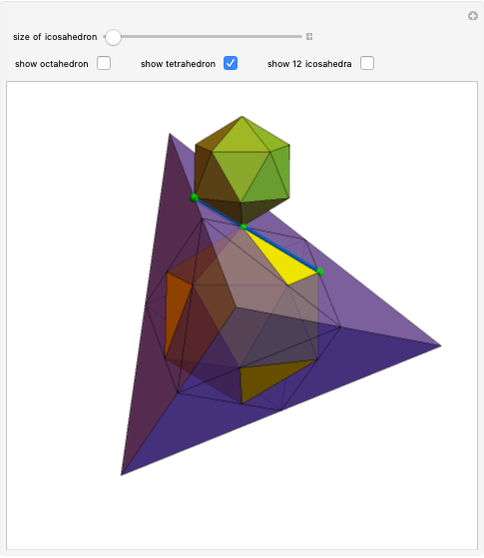
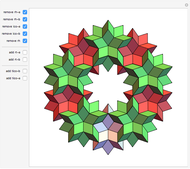
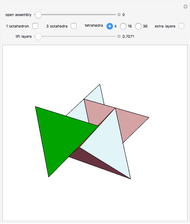
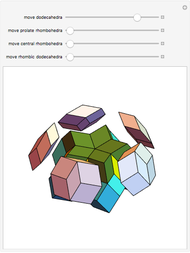
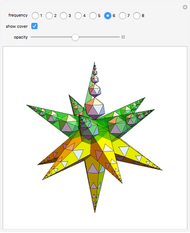
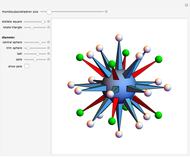
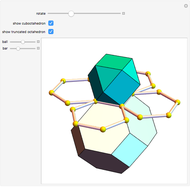
Parts of a rhombic triacontahedron are removed to form a 54-faced space-filling polyhedron. The locations of the removed parts correspond to the vertices of a cube inscribed in the rhombic triacontahedron. Each of the 8 removed parts is equivalent to half of an oblate golden rhombohedron. The faces include 6 golden rhombi and 8x6 triangles. When packed, each space-filling polyhedron has 6+8 neighbors in the direction of faces and vertices of the cube, respectively. The centers of the polyhedra form a body-centered cubic lattice.