Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Conjecture of Apoloniusz Tyszka on the Addition of Rational Numbers

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

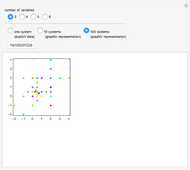
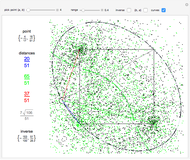
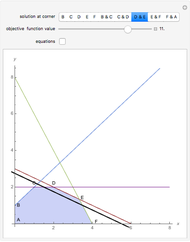
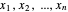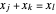This Demonstration illustrates a conjecture of Apoloniusz Tyszka on the set of solutions of a system of linear equations in variables ; the equations are all of the form or for . The conjecture states if such a system has a solution, then there is a solution such that for all .

[more]

The conjecture is illustrated and tested in several ways depending on the value of the parameters set by the user. For a given number of variables, the user can choose a single system, which is selected at random. The system and its unique solution are then displayed in an explicit (textual) form. If the number of systems is larger than one, then the output is displayed graphically in a form that depends on the specified number of variables. For three and four variables a sample of the actual solutions is displayed inside a rectangle or a rectangular box (we omit the first coordinate as it is always 1). For five and six variables the specified number of systems is created at random and the maximal and minimal values from the solution sets are plotted on two bar charts.

[less]

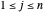Contributed by: Apoloniusz Tyszka (Hugo Kollataj University, Krakow) (March 2011)
Additional work by: Andrzej Kozlowski
Open content licensed under CC BY-NC-SA

Snapshots

Details

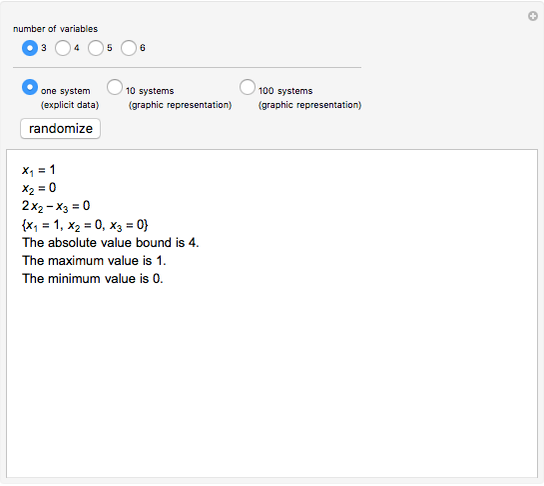
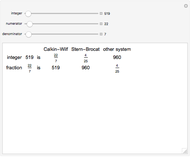
Let 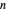be a natural number and 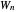denote the set of equations 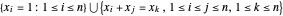. A conjecture of Apoloniusz Tyszka states that any consistent system 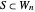has a solution consisting of rationals belonging to 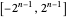. Each consistent system 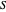of this kind can be enlarged to a system 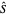with a unique solution. This Demonstration considers these enlarged systems.

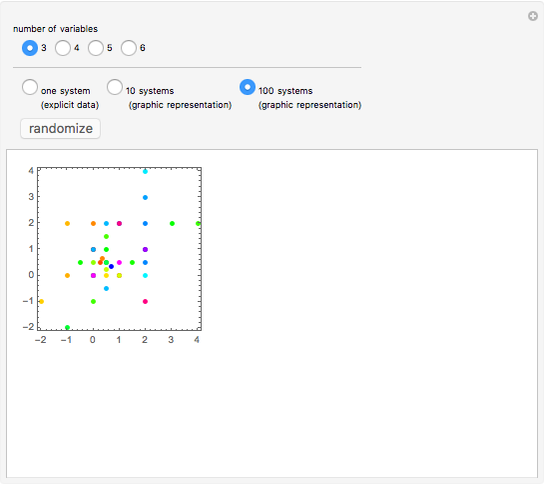
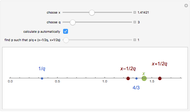
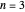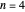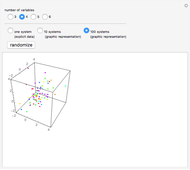
For , there are only 48 solutions, so they are computed and displayed. If you choose 100 systems, there will therefore be no change when you click the randomize button. For , the total number of solutions is still small enough to be computed (confirming the conjecture in this case) but too large to be displayed. Thus the solutions are computed deterministically but a randomly chosen sample is shown. For 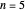and 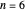, the number of solutions is too large to compute so a random collection of systems is chosen and their maximal and minimal values are displayed on bar charts.

Note that the system of equations:

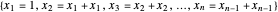
always has the solution , containing a number of the maximal conjectured size.

Reference: A. Tyszka, "Some Conjectures on Addition and Multiplication of Complex (Real) Numbers," arXiv:0807.3010.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send