A Device that Illustrates Pythagoras' Theorem

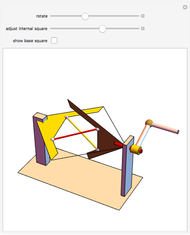
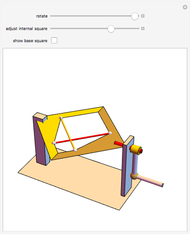
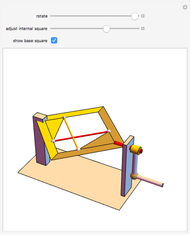
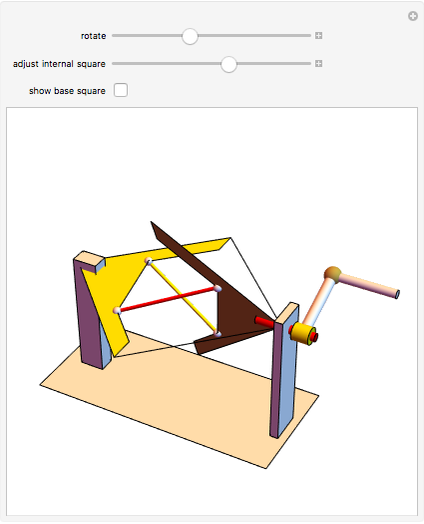
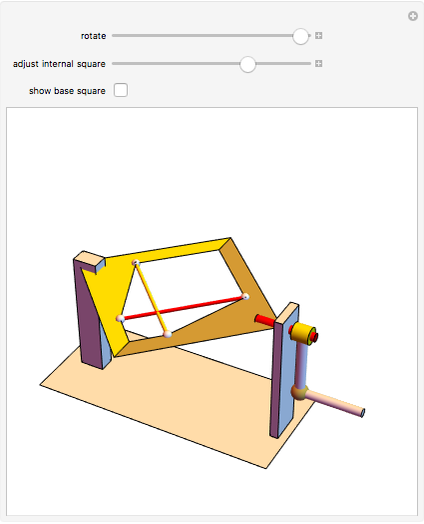
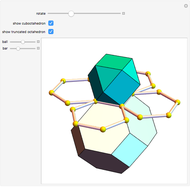
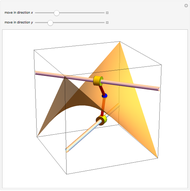
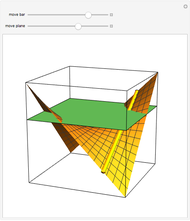
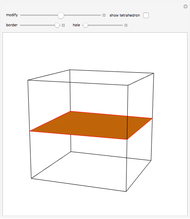
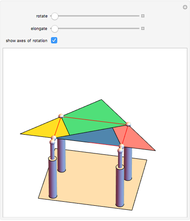
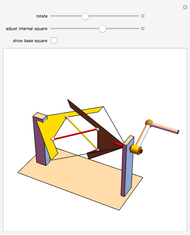
The largest square is split in half by one of its diagonals. A hole is cut out of the square; a base square and an inscribed internal square determine its vertices. Two flexible strings connect the vertices of the internal square. When half of the base square is turned over together with one end of each string, the strings are perpendicular and enclose two smaller squares, whose sum is equal to the original internal square.