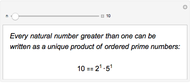
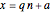A Formula for Primes in Arithmetic Progressions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Let  and
and  be integers with
be integers with  . If
. If  and
and  are relatively prime, then the arithmetic progression
are relatively prime, then the arithmetic progression 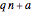 where
where 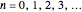 contains an infinite number of primes. The number of such primes that are less than or equal to
contains an infinite number of primes. The number of such primes that are less than or equal to  is a function of
is a function of  usually denoted by
usually denoted by 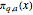 .
.
Contributed by: Robert Baillie (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
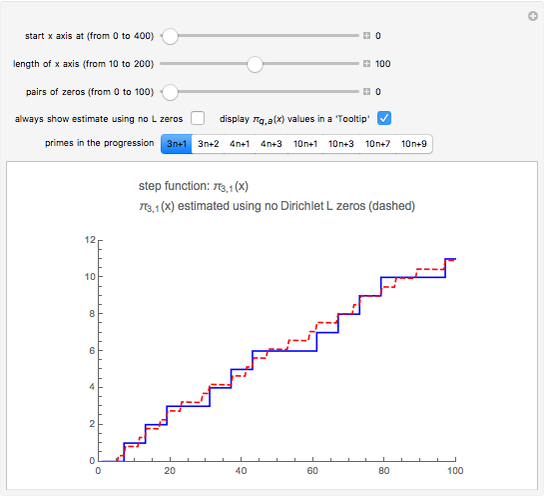
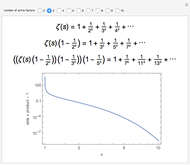
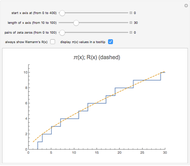
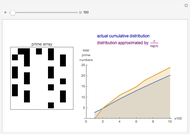
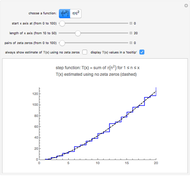
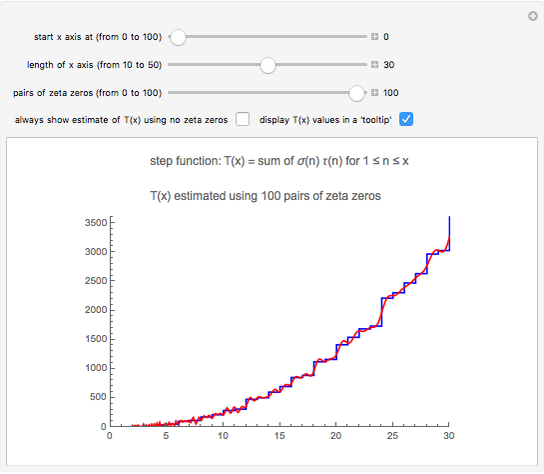
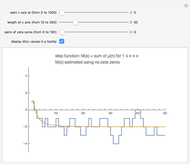
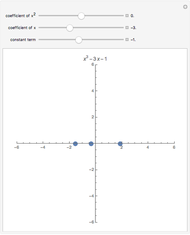
Snapshot 1: primes of the form 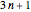 ; the graphs of the step function
; the graphs of the step function 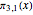 and the formula using no
and the formula using no 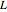 zeros
zeros
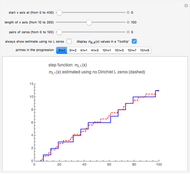
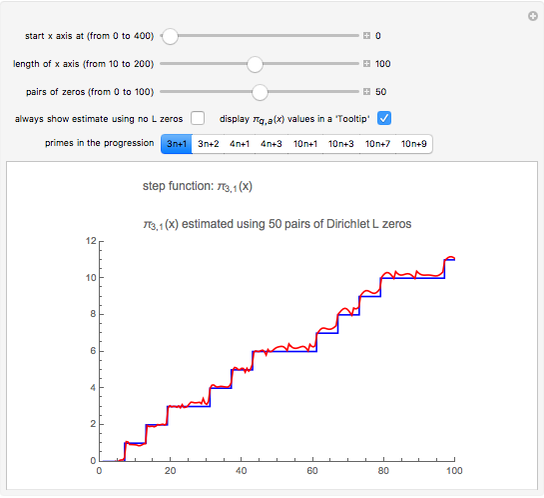
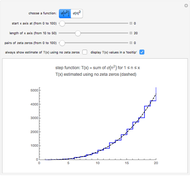
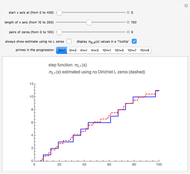
Snapshot 2: the graphs of 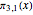 and the formula using 50 pairs of
and the formula using 50 pairs of 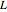 zeros
zeros
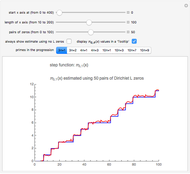
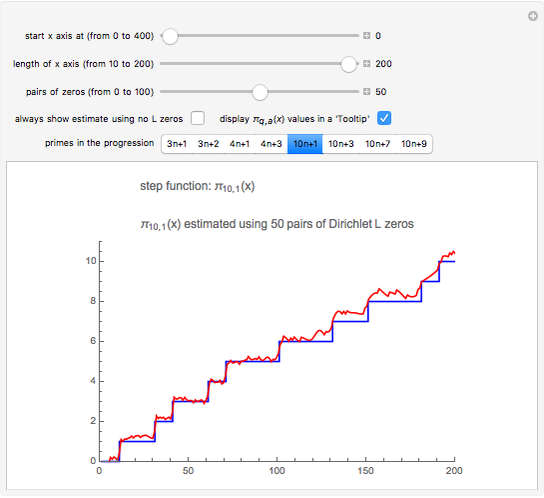
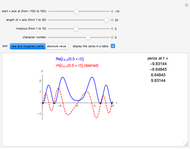
Snapshot 3: primes of the form 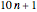 ; the graphs of
; the graphs of 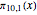 and the formula using 50 pairs of
and the formula using 50 pairs of 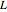 zeros; the step function jumps up at primes 11, 31, 41, 61, 71, …
zeros; the step function jumps up at primes 11, 31, 41, 61, 71, …
Let  and
and  be integers with
be integers with  , and with
, and with  and
and  relatively prime. Dirichlet's theorem (see [3]) says that the arithmetic progression
relatively prime. Dirichlet's theorem (see [3]) says that the arithmetic progression 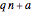 is prime for infinitely many values of
is prime for infinitely many values of  . For example, when
. For example, when 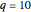 and
and  , the progression
, the progression 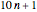 has infinitely many primes, the first five of which are 11, 31, 41, 61, and 71.
has infinitely many primes, the first five of which are 11, 31, 41, 61, and 71.
The standard notation for the number of primes less than or equal to  is
is 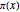 . Likewise, the number of primes in the progression
. Likewise, the number of primes in the progression 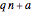 that are less than or equal to
that are less than or equal to  is usually denoted by
is usually denoted by 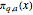 . We will also use Euler's phi (or "totient") function,
. We will also use Euler's phi (or "totient") function, 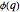 , which is the number of integers between 1 and
, which is the number of integers between 1 and  relatively prime to
relatively prime to  .
.
Technical Details:
These equations come from equations (6)–(8) in reference [1]. There is a lot of terminology here. For an introduction to characters and Dirichlet 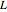 -functions, see reference [3].
-functions, see reference [3].
You use the slider to specify 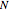 , the number of pairs of complex zeros of Dirichlet
, the number of pairs of complex zeros of Dirichlet 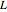 -functions to include in the sums. This Demonstration then applies the following formulas to compute
-functions to include in the sums. This Demonstration then applies the following formulas to compute 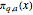 :
:
(1) 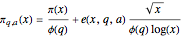 ,
,
where
(2) 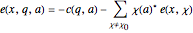 ,
,
(3) 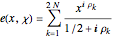 ,
,
and
(4) 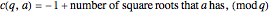
In equation (1), the largest term is 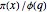 . The other term on the right depends on zeros of
. The other term on the right depends on zeros of 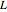 -functions.
-functions.
In equation (2), the asterisk denotes the complex conjugate, and we sum over all characters 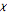 (mod
(mod  ) except the "principal" character,
) except the "principal" character, 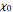 .
.
In equation (3), for the character 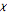 (mod
(mod  ), we sum over
), we sum over 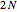 complex zeros of the corresponding Dirichlet
complex zeros of the corresponding Dirichlet 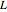 -function. The sum extends over the
-function. The sum extends over the 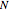 zeros having the smallest positive imaginary part, and the
zeros having the smallest positive imaginary part, and the 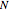 zeros having the least-negative imaginary part. (These pairs of zeros are not necessarily conjugates of each other.)
zeros having the least-negative imaginary part. (These pairs of zeros are not necessarily conjugates of each other.) 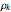 denotes the imaginary part of the
denotes the imaginary part of the  zero. For speed, this Demonstration uses precomputed zeros of
zero. For speed, this Demonstration uses precomputed zeros of 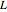 -functions mod 3, 4, and 10.
-functions mod 3, 4, and 10.
In equation (4), if  has no square roots mod
has no square roots mod  (that is,
(that is,  is a quadratic nonresidue mod
is a quadratic nonresidue mod  ), then
), then 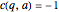 . Otherwise,
. Otherwise,  must have at least two square roots mod
must have at least two square roots mod  ; this makes
; this makes 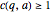 .
.
When equation (1) is graphed, we must account for the fact that, for example, neither of the two progressions mod 3 (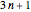 and
and 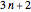 ) include the prime 3. We do this by subtracting 1/2 from each value obtained in equation (1). The same adjustment is made for mod 4, whose progressions omit the prime 2. The mod 10 progressions omit two primes (namely, 2 and 5), so for
) include the prime 3. We do this by subtracting 1/2 from each value obtained in equation (1). The same adjustment is made for mod 4, whose progressions omit the prime 2. The mod 10 progressions omit two primes (namely, 2 and 5), so for 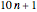 ,
, 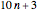 ,
, 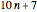 , and
, and 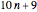 , we subtract 1/4, 0, 3/4, and 1, respectively.
, we subtract 1/4, 0, 3/4, and 1, respectively.
Discussion:
Each of the 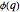 values of
values of  that have no factor in common with
that have no factor in common with  gives rise to an arithmetic progression
gives rise to an arithmetic progression 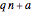 that contains infinitely many primes. As
that contains infinitely many primes. As  approaches infinity, each of these progressions will have the same proportion of primes less than or equal to
approaches infinity, each of these progressions will have the same proportion of primes less than or equal to  . There are
. There are 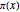 primes less than or equal to
primes less than or equal to  , so each of the
, so each of the 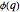 progressions has, as
progressions has, as  approaches infinity, about
approaches infinity, about 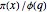 primes. This explains the first term on the right side of equation (1).
primes. This explains the first term on the right side of equation (1).
For example, for  = 10, each of the
= 10, each of the 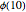 = 4 progressions
= 4 progressions 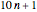 ,
, 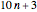 ,
,  , and
, and 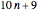 has about
has about 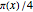 primes, for large
primes, for large  .
.
Notice that equation (1) uses 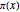 . It might seem like cheating to call something a "formula for primes" when that formula contains
. It might seem like cheating to call something a "formula for primes" when that formula contains 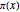 . However,
. However, 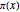 can itself be computed by using a sum of terms that involve zeros of the Riemann zeta function. The Demonstration "How the Zeros of the Zeta Function Predict the Distribution of Primes" shows how to do that.
can itself be computed by using a sum of terms that involve zeros of the Riemann zeta function. The Demonstration "How the Zeros of the Zeta Function Predict the Distribution of Primes" shows how to do that.
Prime Number Races:
As  approaches infinity, each of the
approaches infinity, each of the 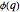 progressions
progressions 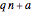 will have the same proportion of primes (namely,
will have the same proportion of primes (namely, 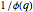 ). However, this does not mean that the progressions have the same number of primes up to any given
). However, this does not mean that the progressions have the same number of primes up to any given  . Perhaps the most dramatic example of this happens with
. Perhaps the most dramatic example of this happens with  . The progressions
. The progressions 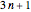 and
and 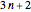 each contain infinitely many primes. The first two primes in these progressions are 2 and 5, both of which belong to the progression
each contain infinitely many primes. The first two primes in these progressions are 2 and 5, both of which belong to the progression 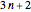 . The next prime is 7, in the progression
. The next prime is 7, in the progression 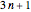 . So, these progressions start out with
. So, these progressions start out with 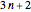 having more primes than
having more primes than 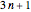 . Using the
. Using the 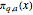 notation, it has been shown that, at least up to
notation, it has been shown that, at least up to  ,
, 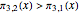 . But here is the amazing part:
. But here is the amazing part: 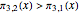 for every
for every  less than 608,981,813,029! At
less than 608,981,813,029! At  = 608,981,813,029,
= 608,981,813,029, 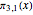 finally exceeds
finally exceeds 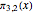 ! In fact,
! In fact,  and
and 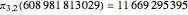 .
.
With the two progressions mod 4, namely, 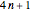 and
and 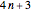 , something similar happens:
, something similar happens: 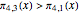 for every
for every  < 26,861. Then, at
< 26,861. Then, at  = 26,861,
= 26,861, 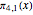 finally becomes greater than
finally becomes greater than 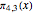 .
.
For 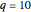 : 3 is prime, so
: 3 is prime, so 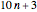 starts out in the lead over the other three progressions
starts out in the lead over the other three progressions 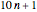 ,
,  , and
, and 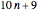 .
. 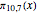 first takes the lead over the other three progressions at
first takes the lead over the other three progressions at 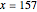 .
. 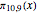 first takes the lead at
first takes the lead at  = 72,269. Finally,
= 72,269. Finally, 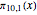 first takes the lead over the other three progressions at
first takes the lead over the other three progressions at  = 45,845,791.
= 45,845,791.
Because each progression mod  has the same proportion of primes, one might expect that the lead would have switched back and forth much more often, as if one were flipping a coin and tallying heads versus tails. It is surprising that one progression so consistently maintains the lead over the others.
has the same proportion of primes, one might expect that the lead would have switched back and forth much more often, as if one were flipping a coin and tallying heads versus tails. It is surprising that one progression so consistently maintains the lead over the others.
For a given  , why do some progressions have more primes than others? The key is equation (4) above. If
, why do some progressions have more primes than others? The key is equation (4) above. If  has no square roots mod
has no square roots mod  (for example,
(for example,  has no square roots mod 3), then
has no square roots mod 3), then 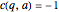 . If
. If  has, say, two square roots mod
has, say, two square roots mod  (for example,
(for example,  has two square roots mod 3), then
has two square roots mod 3), then 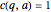 . But if
. But if 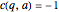 , then, by equation (2),
, then, by equation (2), 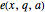 is larger (by 2) than it would be if
is larger (by 2) than it would be if 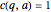 , all other things being equal. This, in turn, makes
, all other things being equal. This, in turn, makes 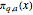 larger when
larger when 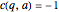 than it would be if
than it would be if 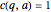 .
.
What this means is that, for values of  that have no square roots mod
that have no square roots mod  , the arithmetic progression
, the arithmetic progression 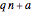 tends to have a few more primes up to a given
tends to have a few more primes up to a given  than other progressions
than other progressions 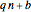 where
where  does have square roots mod
does have square roots mod  . (Of course,
. (Of course, 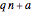 will not have enough primes to affect the proportion, which, as
will not have enough primes to affect the proportion, which, as  approaches infinity, is
approaches infinity, is 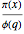 for every progression mod
for every progression mod  .) Finally, it is worth noting that in 1914, Littlewood proved (see reference [2]) that, for both mod 3 and mod 4, the lead switches back and forth infinitely many times.
.) Finally, it is worth noting that in 1914, Littlewood proved (see reference [2]) that, for both mod 3 and mod 4, the lead switches back and forth infinitely many times.
There are many articles about these "prime number races"; for example, [2] is a readable introduction to the subject.
References:
[1] G. Martin, "Asymmetries in the Shanks-Renyi Prime Number Race," arXiv, 2000.
[2] A. Granville and G. Martin, "Prime Number Races," American Mathematical Monthly, 113(1), 2006 pp. 1–33.
[3] W. J. LeVeque, Topics in Number Theory, vol. 2, Reading, MA: Addison–Wesley, 1961 pp. 81–124.
[4] Dirichlet Characteron Wikipedia.
Permanent Citation