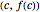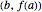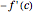Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Generalization of the Mean Value Theorem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

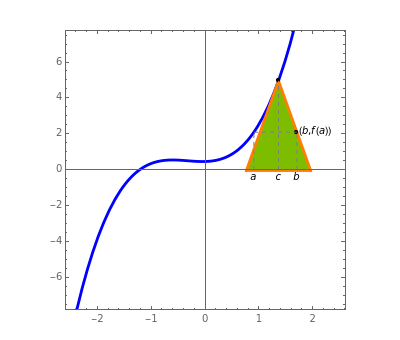
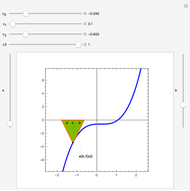
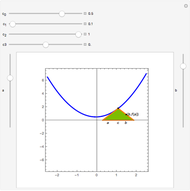
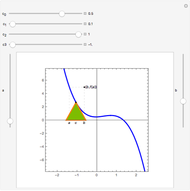
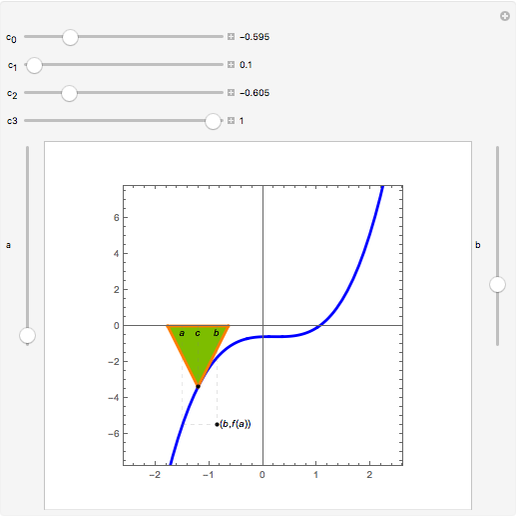
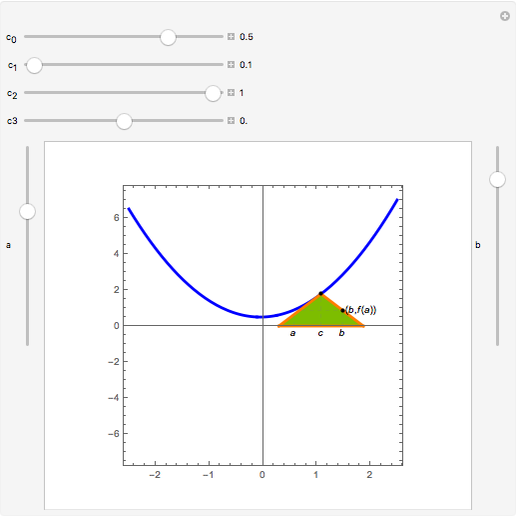
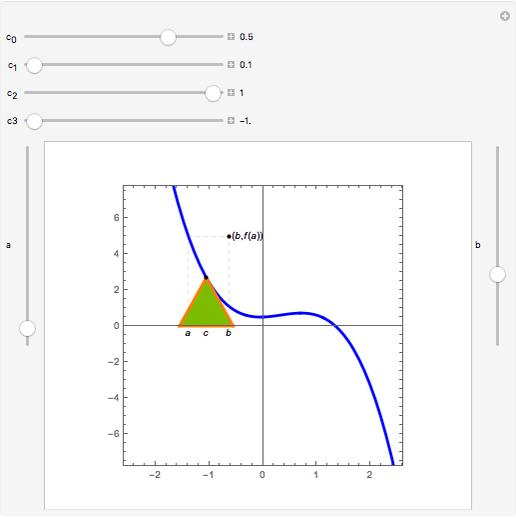
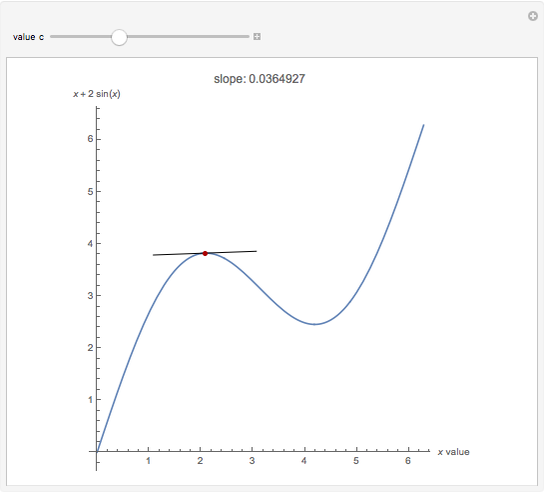
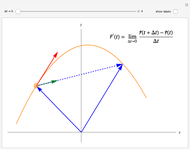
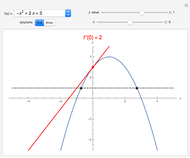
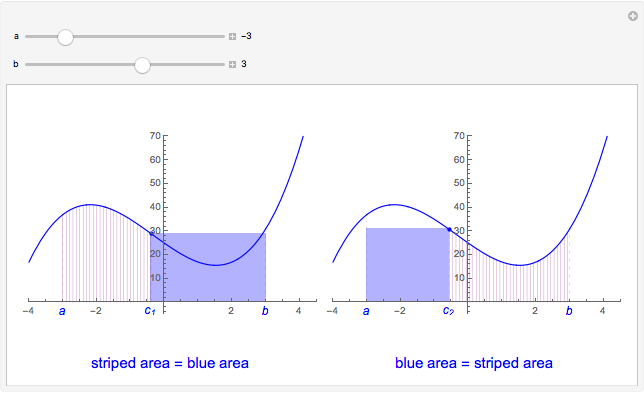
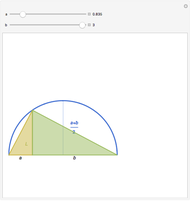
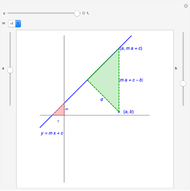
Theorem: Let be a function continuous on 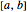and differentiable on . Then there is a in such that .

[more]

Proof: the theorem follows by applying Rolle's theorem to the auxiliary function

Here is a geometric interpretation: The triangle formed by the axis, the tangent line through , and the secant line through and the point is an isosceles triangle (the green triangle). Therefore the slopes of the two sides not on the axis are and .

The example used is the function .

[less]

Contributed by: Soledad Mª Sáez Martínez and Félix Martínez de la Rosa (April 2008)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference: J. Tong, "The Mean-Value Theorem Generalised to Involve Two Parameters," Math. Gazette, 88(513), 2004 pp. 538–540.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send