A Limit Theorem from Information Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
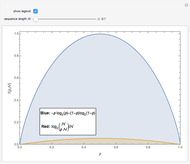
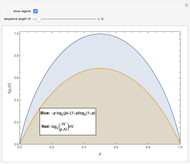
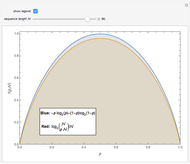
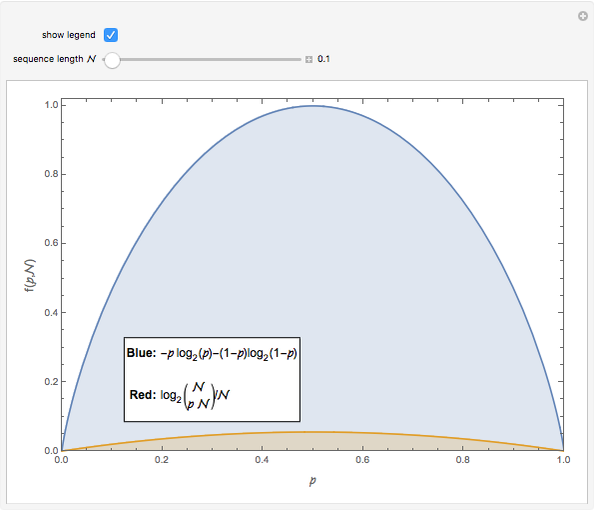
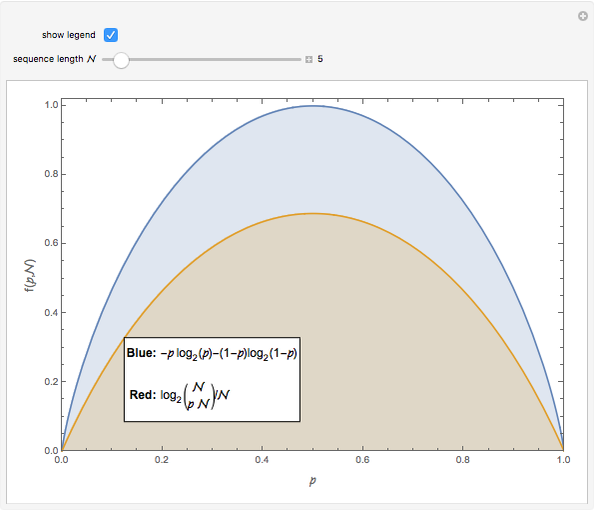
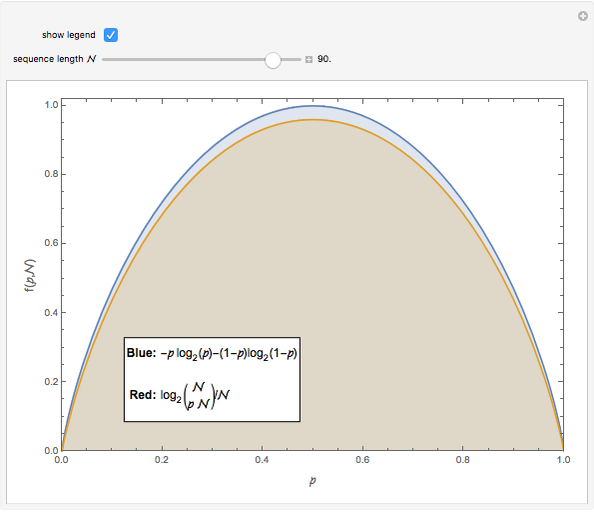
How many distinct sequences can be created by rearranging  binary symbols? If the binary symbols are, say,
binary symbols? If the binary symbols are, say,  and
and  , and if the fraction of
, and if the fraction of  's is denoted
's is denoted  , then the number of possible sequences is
, then the number of possible sequences is 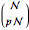 . When
. When  is zero or one there is only one possible sequence for any value of
is zero or one there is only one possible sequence for any value of 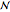 , but when
, but when  , the number of possible sequences increases exponentially with
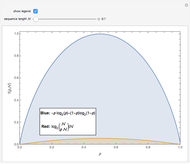
, the number of possible sequences increases exponentially with 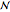 . The logarithm of the number of possible sequences, expressed on a per symbol basis, is
. The logarithm of the number of possible sequences, expressed on a per symbol basis, is 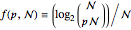 , and the limit
, and the limit 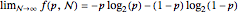 can be interpreted as the average number of bits needed per symbol to describe a long binary sequence with symbol probabilities
can be interpreted as the average number of bits needed per symbol to describe a long binary sequence with symbol probabilities  and
and  . This Demonstration shows
. This Demonstration shows 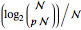 for
for 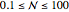 with the limit
with the limit 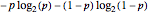 .
.
Contributed by: John Custy (November 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"A Limit Theorem from Information Theory"
http://demonstrations.wolfram.com/ALimitTheoremFromInformationTheory/
Wolfram Demonstrations Project
Published: November 30 2008