A Linear Homogeneous Second-Order Differential Equation with Constant Coefficients

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
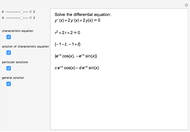
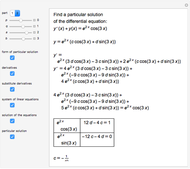
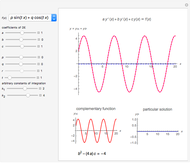
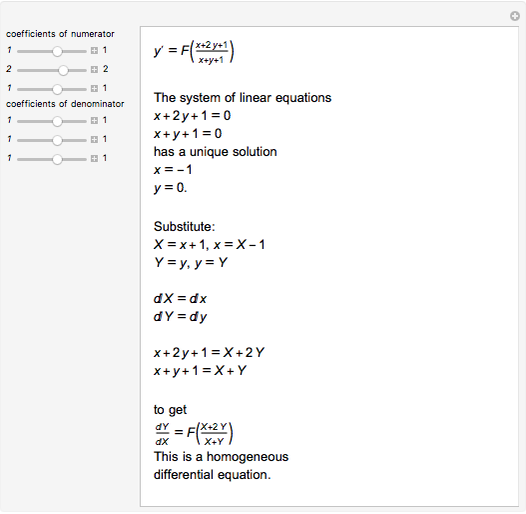
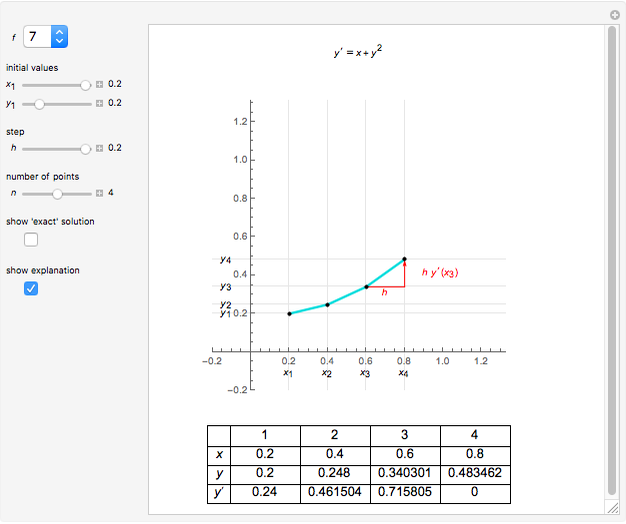
This Demonstration shows how to solve a linear homogeneous differential equation with constant coefficients 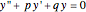 , where
, where 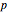 and
and  are constant. First solve the characteristic equation
are constant. First solve the characteristic equation 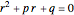 . If
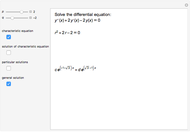
. If  and
and 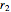 are two real roots of the characteristic equation, then the general solution of the differential equation is
are two real roots of the characteristic equation, then the general solution of the differential equation is 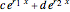 , where
, where  and
and  are arbitrary constants. If
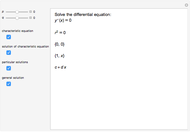
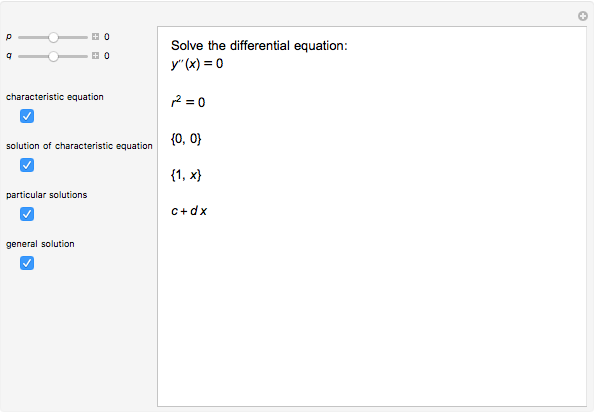
are arbitrary constants. If  , the general solution is
, the general solution is  . If
. If 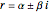 , the general solution is
, the general solution is  .
.
Contributed by: Izidor Hafner (February 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The homogeneous linear differential equation
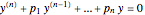
where 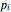 is a function of
is a function of  , has a general solution of the form
, has a general solution of the form
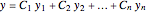 ,
,
where  ,
, 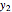 , ...,
, ..., 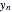 are linearly independent particular solutions of the equation and
are linearly independent particular solutions of the equation and 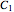 ,
, 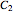 , …,
, …, 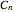 are arbitrary constants.
are arbitrary constants.
If the coefficients 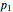 ,
,  , …,
, …, 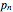 are constant, then the particular solutions are found with the aid of the characteristic equation
are constant, then the particular solutions are found with the aid of the characteristic equation
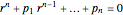 .
.
To each real root 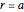 of the characteristic equation of multiplicity
of the characteristic equation of multiplicity 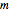 , there corresponds
, there corresponds 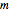 particular solutions
particular solutions 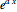 ,
, 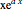 , …,
, …, 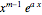 .
.
To each pair of imaginary roots 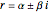 of multiplicity
of multiplicity 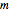 , there corresponds
, there corresponds 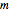 pairs of particular solutions
pairs of particular solutions
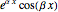 ,
,  ,
,
 ,
, 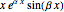 ,
,
…
 ,
,  .
.
Reference
[1] V. P. Minorsky, Problems in Higher Mathematics, Moscow: Mir Publishers, 1975 p. 261.
Permanent Citation