A Massive Bar Oscillating between Two Identical Rotating Support Rollers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
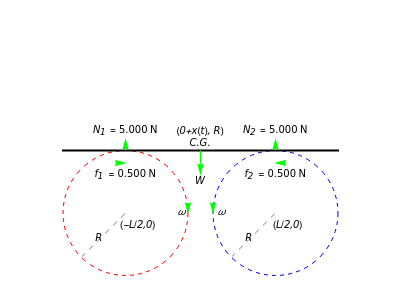
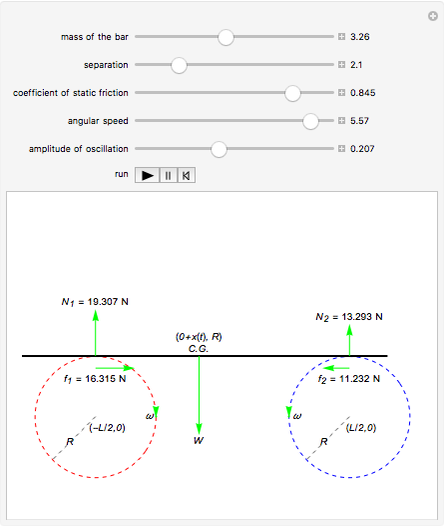
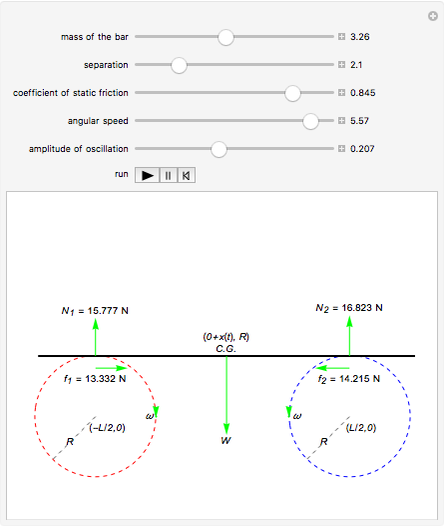
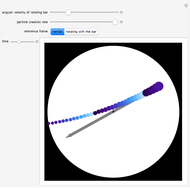
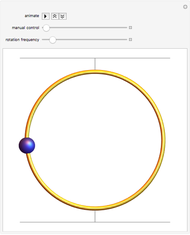
A heavy uniform bar of mass 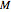 rests on top of two identical rollers that are continuously and rapidly turned in opposite directions with angular speed
rests on top of two identical rollers that are continuously and rapidly turned in opposite directions with angular speed  . The centers of the rollers are at a distance
. The centers of the rollers are at a distance 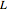 apart. The coefficient of kinetic friction between the bar and the roller surfaces is
apart. The coefficient of kinetic friction between the bar and the roller surfaces is  , a constant independent of the relative speed of the two surfaces. The bar, held at rest with its center at distance
, a constant independent of the relative speed of the two surfaces. The bar, held at rest with its center at distance 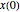 from the midpoint of the two rollers, is released at
from the midpoint of the two rollers, is released at  . This Demonstration depicts the subsequent motion.
. This Demonstration depicts the subsequent motion.
Contributed by: Anindya Kumar Biswas (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
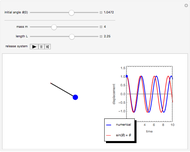
The motion obeys the differential equation, 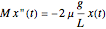 ;
; 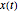 is the position of the center of gravity from the midpoint of the two rollers at an instant
is the position of the center of gravity from the midpoint of the two rollers at an instant  .
.
The bar executes simple harmonic motion, 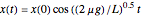 , for all amplitudes
, for all amplitudes 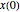 .
.
Notation:
C.G. is the center of gravity.
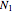 and
and 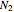 are the normal forces acting on the bar through the points of the contact with the left and right cylinders,
are the normal forces acting on the bar through the points of the contact with the left and right cylinders, 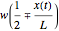 .
.
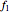 and
and 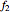 are the kinetic frictional forces at the left and right contact points on the bar,
are the kinetic frictional forces at the left and right contact points on the bar, 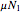 and
and 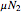 .
.
Reference: D. Kleppner and R. J. Kolenkow, An Introduction to Mechanics (Special Indian Edition), India: Tata McGraw–Hill, 1999 problem 6.9.
Permanent Citation