A Model for Pedestrian Interaction with Anticipation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
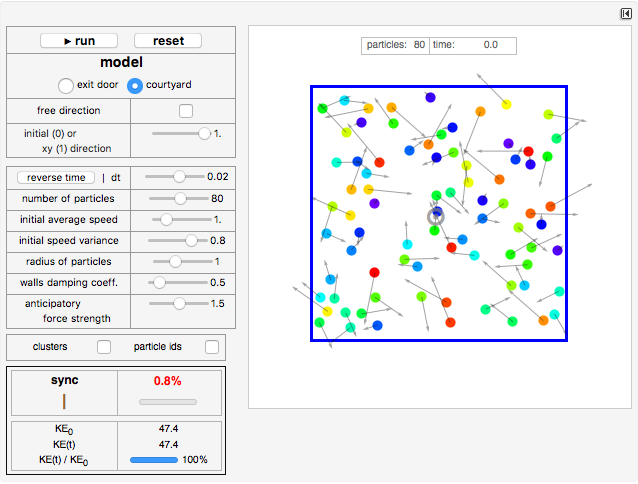
This model represents a crowd of pedestrians and their interactions [1].
[more]
Contributed by: Luca Moroni (March 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
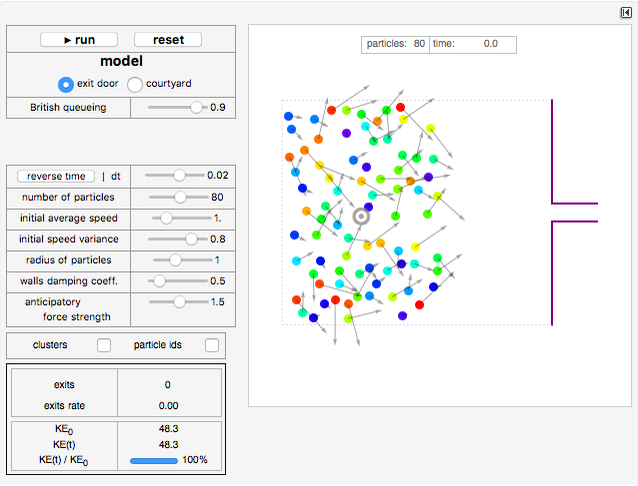
Controls
"dt": Time step used in the integrator; higher values make the simulation run more quickly but less precisely.
"initial speed variance": The interval for the initial speeds (randomly generated with a uniform distribution) is (1±variance) times the initial average speed.
"walls damping coeff.": If this coefficient is set to 0, there is no damping when the particles bounce against the walls, reproducing a pure elastic collision. Otherwise the damping coefficient reduces the elastic bouncing behavior of the particles, creating potentially interesting clustering and synchronization effects.
"anticipatory force strength": Multiplicative coefficient for the strength of the anticipatory force in the pedestrians' interactions.
"courtyard" model
"free direction": Particles have no preferred direction and move freely after each interaction.
"initial (0) or xy (1) direction": Coefficient to change (mix) the behavior from the initial velocity preferred direction (0) to horizontal/vertical preferred direction (1). In the first case, to allow for a "natural" bouncing, the preferred direction angles for the velocity vector at time  will be
will be 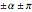 , where
, where  is the initial vector angle.
is the initial vector angle.
"exit door" model
"British queueing": Coefficient to shift back the target points of each particle (according to their position) from the exit door in order to form a more ordered queue in the British style. After entering the "ideal" queue, the particles move toward the exit door.
Indicators
"energy": Since the pedestrian interaction force is not conservative, energy is not preserved and particles would then slow down and lose all of their initial kinetic energy. To avoid this, all the particles are given a "restoring speed" force and then try to regain their initial absolute speeds after each interaction. The difference between the initial kinetic energy and the actual kinetic energy represents the energy currently absorbed in the interactions.
"particle ids": Red particles have higher speeds, blue particles have lower speeds, and other colors have intermediate speeds proportional to their hue color.
"clusters": If this option is checked, clusters are shown as gray dotted circles, where the line thickness/darkness is proportional to the cluster size. Clusters are calculated through the Mathematica function FindClusters.
"sync" (only shown in the "courtyard model"): This index is higher when the particles tend to circulate around the center of mass with the same rotational direction. It would be 100% if all the particles rotated in the same clockwise (red) or counterclockwise (blue) direction around the center of mass.
"exits rate" (only shown for the "exit door model"): Number of exits per unit time. The time is calculated from the time of the first exit minus 4.
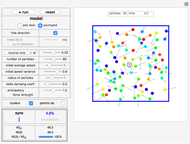
Snapshot 1: In the "courtyard" environment, after the initial random and disordered interactions, particles tend to move in a synced circular motion and form clusters.
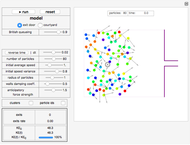
Snapshot 2: In the "exit door" environment with the British queueing control set close to 1, particles tend to form an ordered queue.
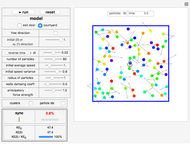
Snapshot 3: In the "exit door" environment with the British queueing control set close to zero, particles crowd in a disorderly way in front of the exit door. This queueing style usually produces a lower exit rate than that of the British style.
The Verlet discrete time integrator was adapted from a Demonstration by Ulrich Mutze and Stephan Leibbrandt (Approach of a System of Particles towards Thermal Equilibrium; see Related Links).
References
[1] I. Karamouzas, B. Skinner, and S. J. Guy, "Universal Power Law Governing Pedestrian Interactions," Physical Review Letters, 113, 238701, 2014. journals.aps.org/prl/abstract/10.1103/PhysRevLett.113.238701.
[2] S. Strogatz, Sync: The Emerging Science of Spontaneous Order, New York: Hyperion, 2003.
[3] L. Moroni. "An Anticipatory Interaction Model for a Crowd of Pedestrians." (Mar 1, 2015) www.lucamoroni.it/cdf-simulations/anticipatory-interaction-model-for-pedestrians.
Permanent Citation
"A Model for Pedestrian Interaction with Anticipation"
http://demonstrations.wolfram.com/AModelForPedestrianInteractionWithAnticipation/
Wolfram Demonstrations Project
Published: March 26 2015