A Nonlinear Model for the Rings of Saturn

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
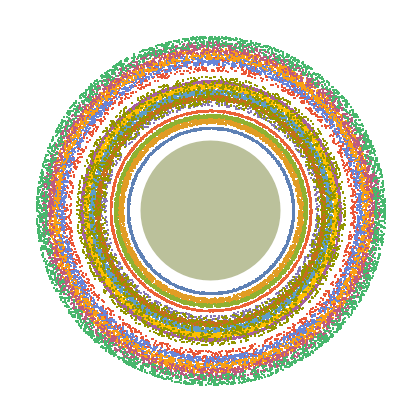
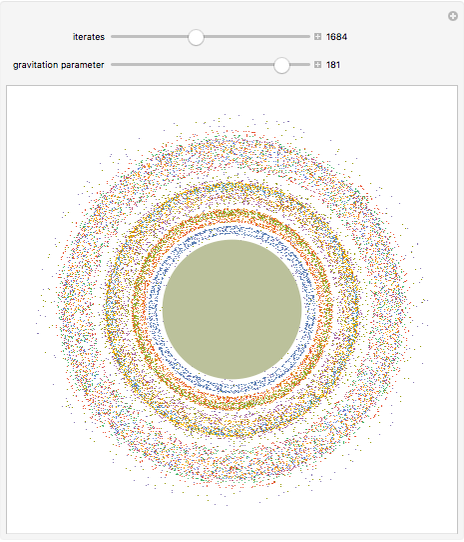
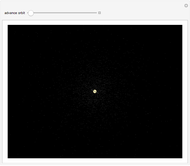
This is a nonlinear mapping for a qualitative simulation of the rings of Saturn. The model is due to Fröyland, from considerations of the Roche limit for the case of the moon Mimas.
Contributed by: Enrique Zeleny (March 2012)
Open content licensed under CC BY-NC-SA
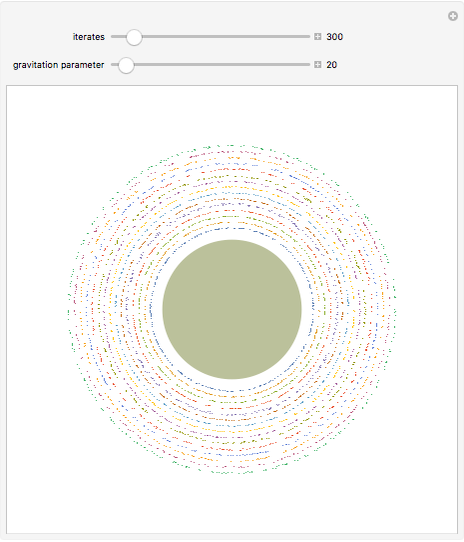
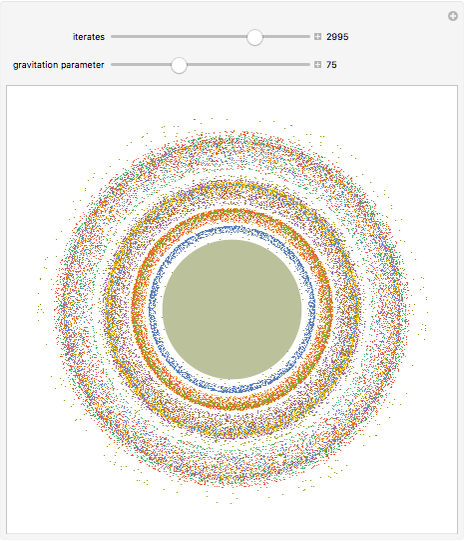
Snapshots
Details
Converting the differential equation of the model to a pair of finite-difference equations, we find
 ,
,
 ,
,
where  is the radial distance from the center of Saturn to Mimas,
is the radial distance from the center of Saturn to Mimas,  and
and  are the radial and angular positions of a ring particle after
are the radial and angular positions of a ring particle after  revolutions, and
revolutions, and  is a gravitation parameter derived from Newton's law of gravitation and Kepler's third law.
is a gravitation parameter derived from Newton's law of gravitation and Kepler's third law.
Reference
[1] R. H. Enns and G. C. McGuire, Nonlinear Physics with Mathematica for Scientists and Engineers, Boston: Birkhäuser, 2001.
Permanent Citation