Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Parallelogram Defined by the Centers of Four Incircles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

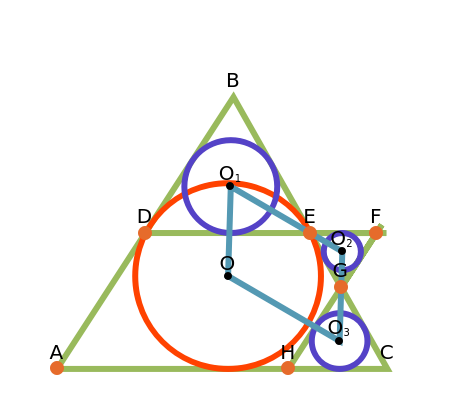
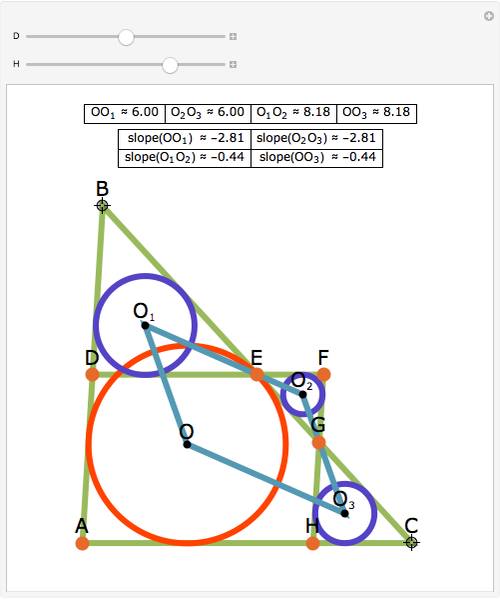
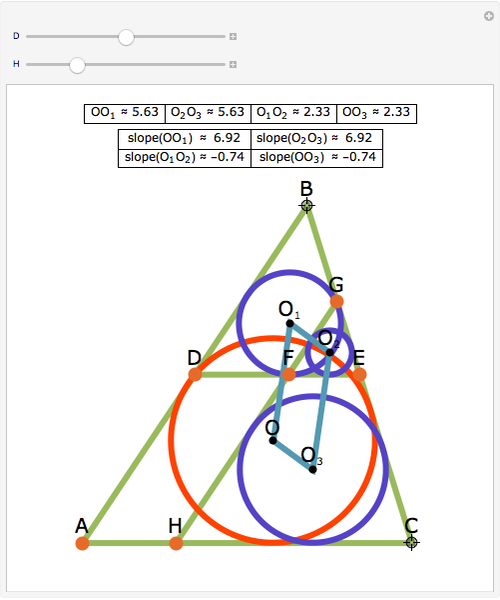
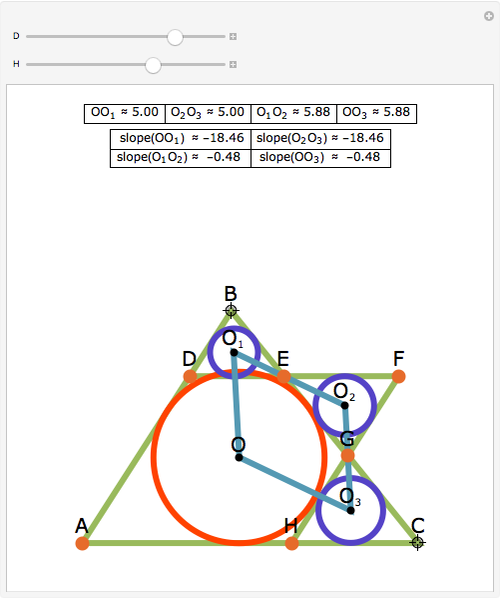
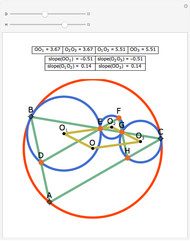
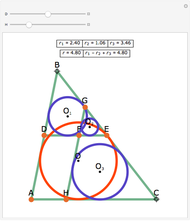
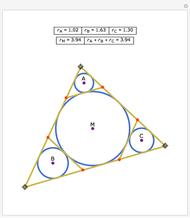
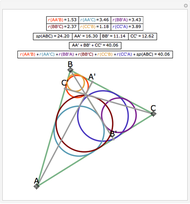
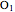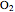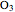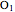
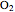
Let ABC be a triangle. Let the line DEF be parallel to AC with D on AB and E on BC. Let the line FGH be parallel to AB with H on AC and G on BC. Let O, , , and be the incircles of the triangles ABC, DBE, FEG, and CGH, respectively. Then O is a parallelogram.

Contributed by: Jay Warendorff (March 2011)
After work by: Antonio Gutierrez
Open content licensed under CC BY-NC-SA

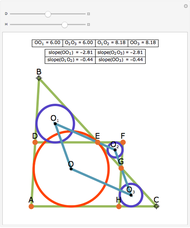
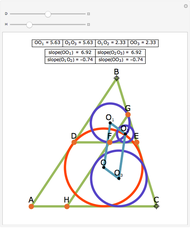
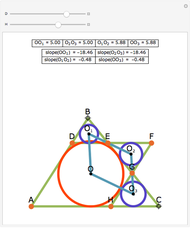
Snapshots

Details

The statement of the theorem is in Problem 96. Similar Triangles, Incenters, Parallelogram.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send