A Procedure to Compute the Digit Sequence of a Rational Number

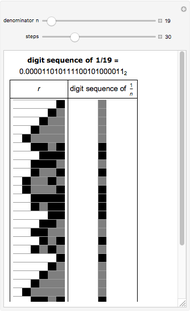
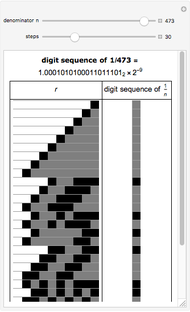
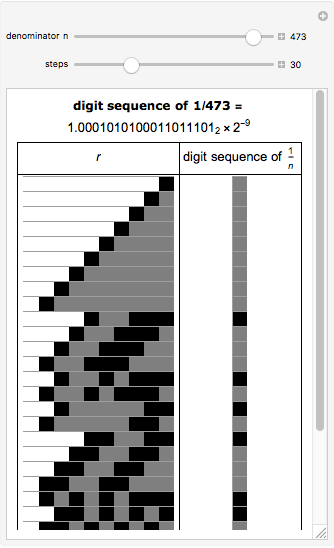
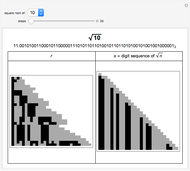
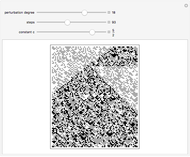
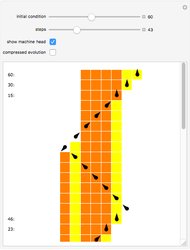
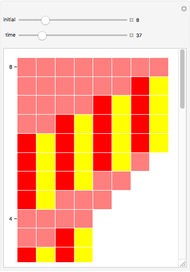
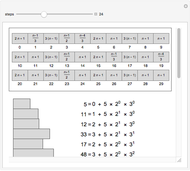
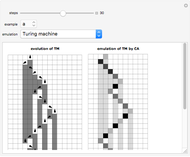
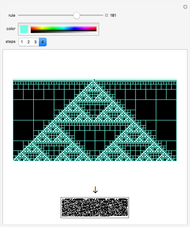
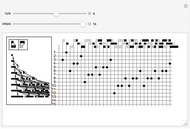
This Demonstration visualizes a procedure for generating the base 2-digit sequence for the rational number , , . From A New Kind of Science, p. 139: "The idea is to have a number which essentially keeps track of the remainder at each step in the division. One starts by setting equal to . Then at each step, one compares the values of and . If is less than , the digit generated at that step is 0, and is replaced by . 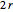Otherwise, is replaced by . With this procedure, the value of is always less than . 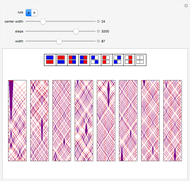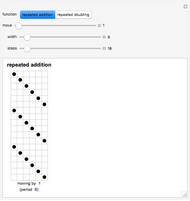And as a result, the digit sequence obtained always repeats at most every steps." On the left, the row shows the binary digits of at the step in the algorithm, and on the right, the binary digits of 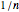are shown vertically. Black cells represent 1's, and gray cells represent 0's.