A Proof of Euler's Formula

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
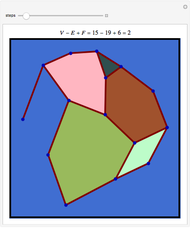
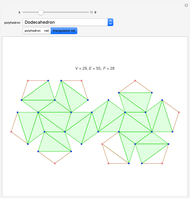
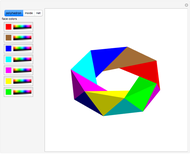
Euler's formula states that for a map on the sphere,  , where
, where  is the number of vertices,
is the number of vertices,  is the number of faces, and
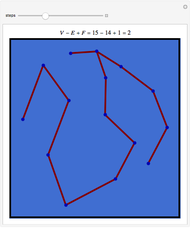
is the number of faces, and  is the number of edges. This Demonstration shows a map in the plane (so the exterior face counts as a face). The formula is proved by deleting edges lying in a cycle (which causes
is the number of edges. This Demonstration shows a map in the plane (so the exterior face counts as a face). The formula is proved by deleting edges lying in a cycle (which causes  and
and  to each decrease by one) until there are no cycles left. Then one has a tree, and one can delete vertices of degree one and the edges connected to them until only a point is left. Each such move decreases
to each decrease by one) until there are no cycles left. Then one has a tree, and one can delete vertices of degree one and the edges connected to them until only a point is left. Each such move decreases  and
and  by one. So all the moves leave
by one. So all the moves leave  unchanged, but at the end
unchanged, but at the end  and
and  are each 1 and
are each 1 and  is 0, so
is 0, so  must have been 2 at the start.
must have been 2 at the start.
Contributed by: Stan Wagon (Macalester College) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"A Proof of Euler's Formula"
http://demonstrations.wolfram.com/AProofOfEulersFormula/
Wolfram Demonstrations Project
Published: March 7 2011