A Remarkable Formula Of Ramanujan

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
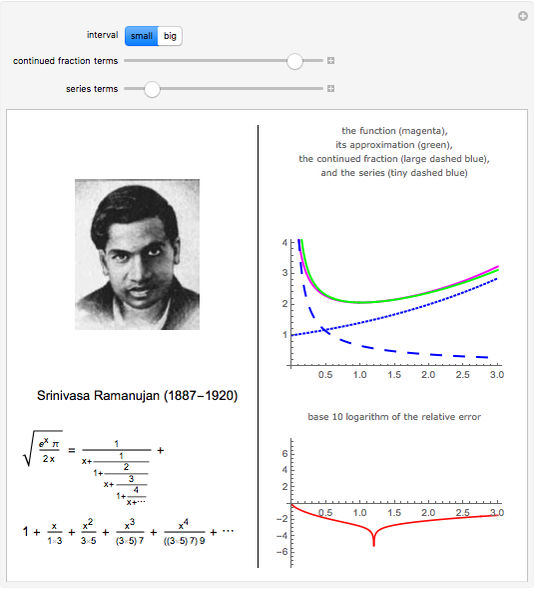
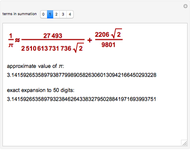
The function 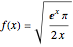 (for
(for 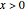
 ) can be decomposed into a sum of a continued fraction and a series. The best-known case of this formula corresponds to
) can be decomposed into a sum of a continued fraction and a series. The best-known case of this formula corresponds to 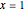 . It is surprising that, separately, neither the continued fraction nor the series can be expressed in terms of
. It is surprising that, separately, neither the continued fraction nor the series can be expressed in terms of  or
or  . When
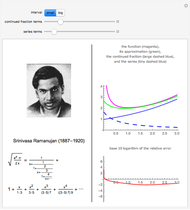
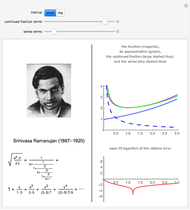
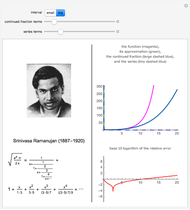
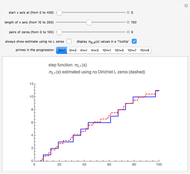
. When  is not too big, both the continued fraction and the series significantly contribute to the approximation
is not too big, both the continued fraction and the series significantly contribute to the approximation 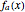 (in green) of
(in green) of  (in magenta); for large values of
(in magenta); for large values of  , the contribution comes nearly exclusively from the series. This can be seen in the first graph, using the "small" or the "big" interval. In the second graph, the base 10 logarithm of the relative error
, the contribution comes nearly exclusively from the series. This can be seen in the first graph, using the "small" or the "big" interval. In the second graph, the base 10 logarithm of the relative error  is shown, which corresponds to the digit in which the error appears (higher negative means more precision).
is shown, which corresponds to the digit in which the error appears (higher negative means more precision).
Contributed by: Juan Luis Varona (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"A Remarkable Formula Of Ramanujan"
http://demonstrations.wolfram.com/ARemarkableFormulaOfRamanujan/
Wolfram Demonstrations Project
Published: March 7 2011