A Simple Model for Leaf Placement
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
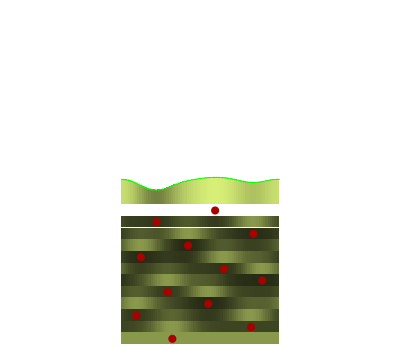
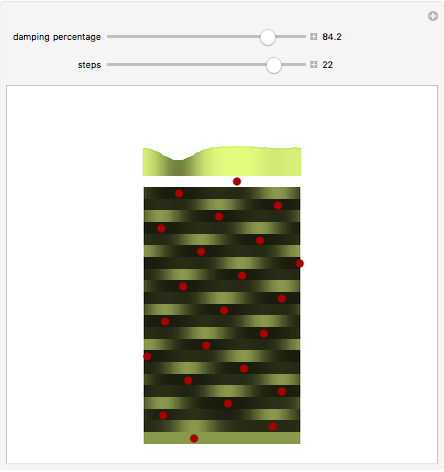
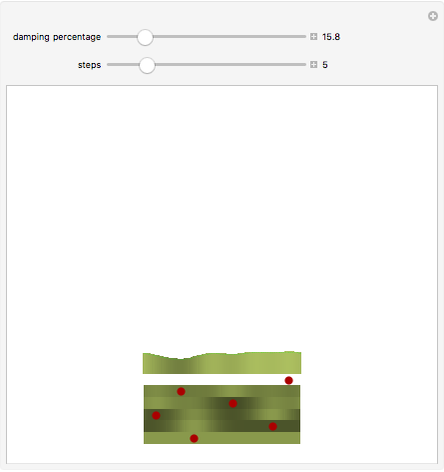
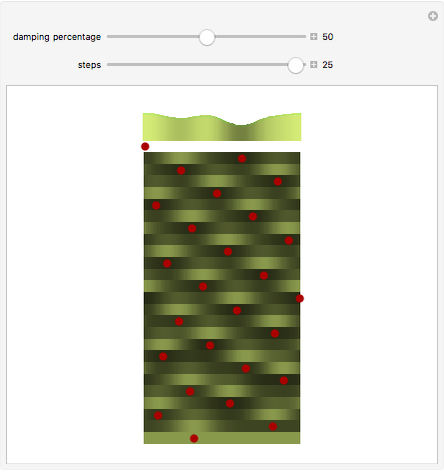
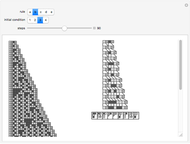
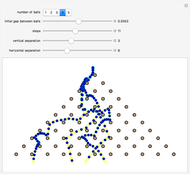
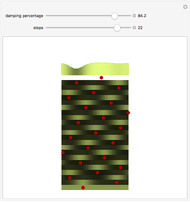
This Demonstration is a simple model of how leaves are placed on a plant stem. Sections of the cylindrical stem are unrolled into horizontal lines; the stem grows up the page. The red dots are where new leaves start to grow. The concentration of some hypothetical growth chemical is denoted by the curve at the top with varying shades of green. New leaves grow where the concentration of this chemical is the highest (i.e. lightest green) on the stem. This red dot is assumed to decrease the concentration around it, but overall concentration is increased before the next step. For more information, see Details.
Contributed by: Abigail Nussey (March 2011)
Based on a program by: Ed Pegg Jr.
Open content licensed under CC BY-NC-SA
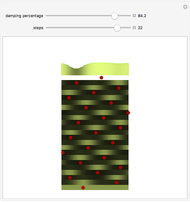
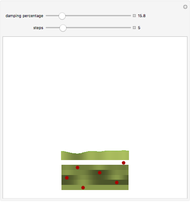
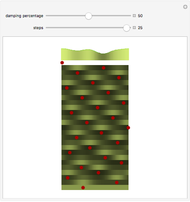
Snapshots
Details
The angles between successive elements correspond to the horizontal distance between the two elements. Though these angles vary for the first few steps, there is, for most damping percentages, a rapid convergence to a fixed distance corresponding to an angle of almost exactly 137.5°.
The "damping percentage" refers to the damping of the memory of the previous position on the stem. When all memory is damped out (damping percentage = 100%), successive elements form 180° angles. Where there is very little damping, elements form at relatively random angles.
Phyllotaxis spirals are examples of structures whose successive elements are added at the golden ratio angle 137.5°.
For more information, see Stephen Wolfram's A New Kind of Science, pp. 400–412.
Permanent Citation
"A Simple Model for Leaf Placement"
http://demonstrations.wolfram.com/ASimpleModelForLeafPlacement/
Wolfram Demonstrations Project
Published: March 7 2011
Simple Probabilistic Cellular Automata
Abigail Nussey
Complex Networks from Simple Rewrite Rules
Richard Southwell
Tumor Growth Model
Enrique Zeleny
Neighbor-Dependent Network Systems
Abigail Nussey
Multiway Systems
Abigail Nussey
Two Types of Network Systems
Abigail Nussey
Symbolic Systems
Abigail Nussey
Cyclic Tag Systems
Abigail Nussey
Tag Systems
Abigail Nussey
Multicolor Neighbor-Dependent Substitution Systems
Abigail Nussey
-
Paths of Balls Bouncing Off Pegs
Abigail Nussey -
Neighbor-Dependent Network Systems
Abigail Nussey -
Four-Color Outer Median Cellular Automata on Graphs
Abigail Nussey -
Emulation of a Register Machine by an Arithmetic System Rule
Abigail Nussey -
Three-Color Block Cellular Automata
Abigail Nussey -
Huffman Encoding
Abigail Nussey -
Repeated Addition and Doubling
Abigail Nussey -
Emulating Other Systems with Cellular Automata
Abigail Nussey -
Two-Dimensional Neighbor-Dependent Substitution Systems
Abigail Nussey -
Huffman Encoding of the Evolution of a Cellular Automaton
Abigail Nussey -
Simple Probabilistic Cellular Automata
Abigail Nussey -
Emulation of a Multicolor Turing Machine by a Two-Color Turing Machine
Abigail Nussey -
Randomized Evolutions of Continuous Cellular Automata Generalizing Rules 30 and 90
Abigail Nussey -
Causal Network Generated by a Mobile Automaton
Abigail Nussey -
Random Walks on Various Topologies
Abigail Nussey -
Sequential Substitution Networks
Abigail Nussey -
Two-Dimensional Recursive Subdivision of the Evolution of a Cellular Automaton
Abigail Nussey -
Strings That Are Derivable in a Certain Number of Steps by a Multiway System
Abigail Nussey -
A Simple Model for Leaf Placement
Abigail Nussey -
Emulation of Elementary Cellular Automata by a Universal Cellular Automaton
Abigail Nussey