A Two-Phase Anneal: The Beauty of Interface Dynamics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
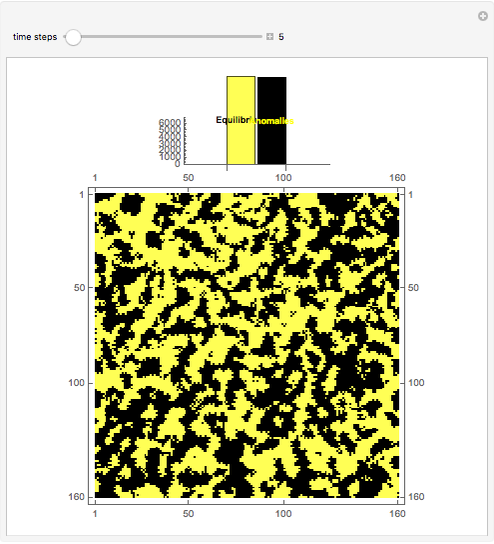
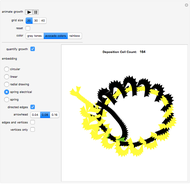
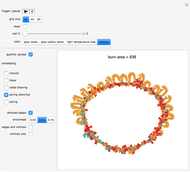
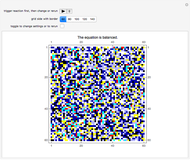
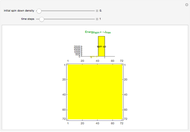
Two phases are tracked as they tend toward single-phase homogeneity as a consequence of an interface dynamic acting like surface tension. Roughly speaking, this dynamic is observed to act in such a way as to "squeeze out" one of the phases over time. The yellow phase is intended to represent some given solid material's nonanomalous regions, while the black phase is intended to represent any one of various possible anomalies in the material, such as dislocation or other defect, and the stresses they produce. In consideration of experiment, the observed tendency of this abstraction to progress toward its nonanomalous equilibrium state configuration would be consistent with an elevated temperature anneal that similarly would tend to drive a given system toward its nonanomalous equilibrium state configuration through the diffusive relocation of atoms within the material (microstructure anneal), which in turn would facilitate stress relief (stress anneal); the latter would appear as a lowering of the material's Gibbs energy. A key point of observation is the model's proposed atomic diffusion through the interfaces between the phases; when the control variable "time steps" is zero, the number of such interfaces is a maximum.
Contributed by: Michael Dewus (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
All the rich action takes place at the interfaces between the phases in this model; it follows that the attendant macroscopic picture could be envisioned as a dynamic buildup of "discrete interfaces". The interfaces, of varying radii of curvature, collapse into one another with time. The surface tension-like dynamic that acts at a given interface is a consequence of cellular automaton nine-neighbor totalistic rule 976, which itself precludes interesting behavior in the uniform regions of the phases to the extent that the dynamic at the interfaces carves out the observed geometries. Rule 976 is a very simple contrarian-like totalistic rule that sets a given cell to a state that is the opposite of that for which its nine-neighbor neighborhood (including self) is a marginal majority—specifically, neighborhood sum 4 is set to 1 (the 0's marginal majority with respect to sum 9), and neighborhood sum 5 is set to 0 (the 1's marginal majority with respect to sum 9), while nonmarginal majority summations remain at the state representative of that particular nonmarginal majority. This marginality consideration is an important feature of rule 976 and explains the rich behavior observed at the interfaces; moreover, the rule's nine-neighbor kernel is the kernel of choice owing to its relatively more comprehensive interface overlay capability. As time increases, convex protrusions are observed to recede, which means that the phase associated with that protrusion diminishes while the other commensurately increases; given enough time in which the automaton works, the yellow nonanomalous equilibrium-state phase begins to dominate, which is consistent with a temperature cycling or other work-related anneal that alters microstructure and relieves stress so as to drive a system toward its relatively more defect and stress-free equilibrium state. In this model the initial conditions are random, but consistent seeding always leads to the yellow phase inevitably becoming the equilibrium state representative as the control variable approaches its maximum value; the bar chart atop the phase picture quantifies the phase residuals as the control variable increments. The source code has been liberally commented to offer further programmatic clarity.
See Annealing (particularly, Metallurgy: Thermodynamics).
References
[1] B. Chopard and M. Droz, Cellular Automata Modeling of Physical Systems, Cambridge: Cambridge University Press, 2005.
[2] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, Inc., 2002.
Permanent Citation
"A Two-Phase Anneal: The Beauty of Interface Dynamics"
http://demonstrations.wolfram.com/ATwoPhaseAnnealTheBeautyOfInterfaceDynamics/
Wolfram Demonstrations Project
Published: August 5 2011