Adding a Second Component to a Fixed-Volume Container

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
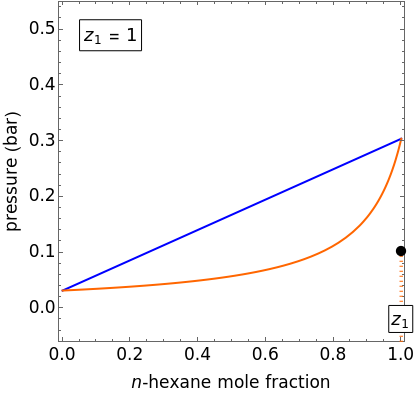
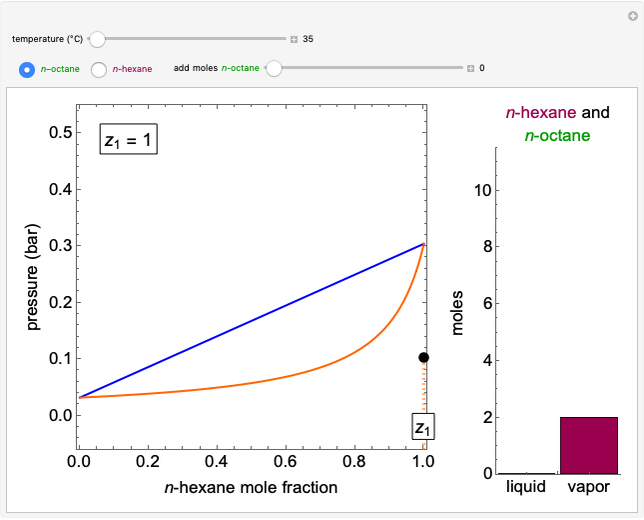
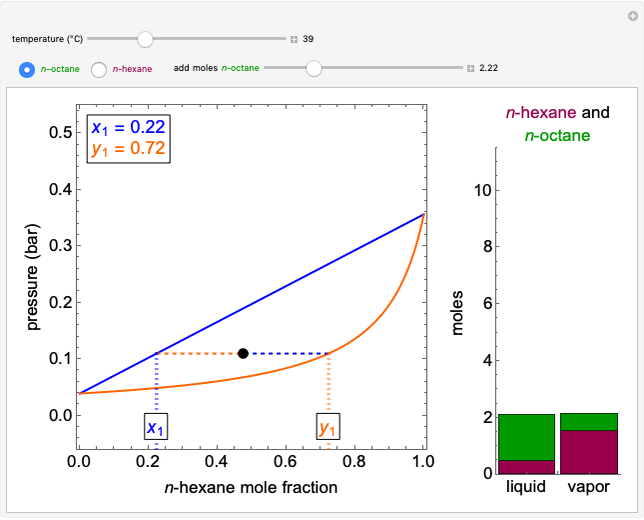
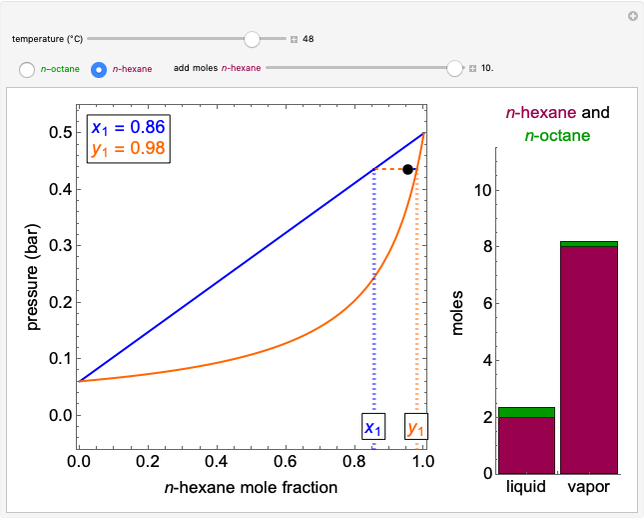
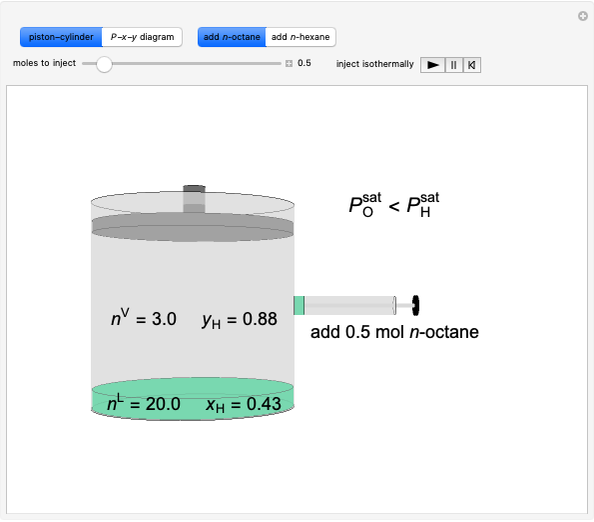
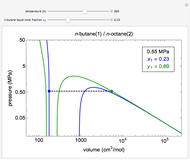
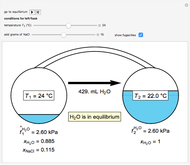
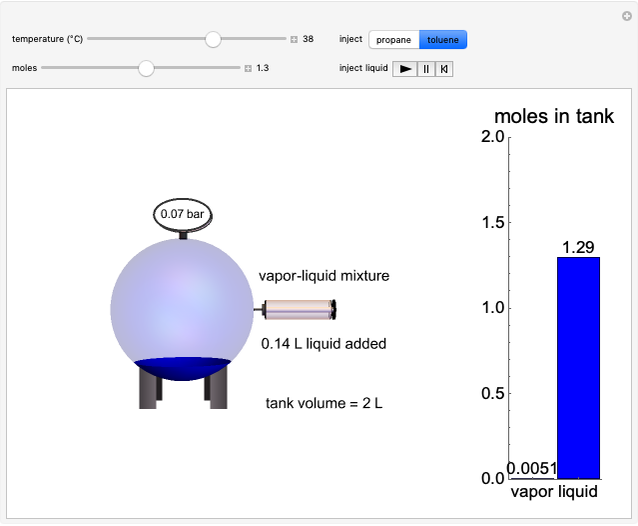
A constant-volume tank initially contains one component in the vapor phase (either 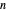 -octane or
-octane or 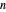 -hexane), and you can add the other component at constant temperature using a slider. Change the temperature with another slider. Select the component to be added with buttons. The pressure-composition
-hexane), and you can add the other component at constant temperature using a slider. Change the temperature with another slider. Select the component to be added with buttons. The pressure-composition 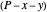 diagram has a blue line for the bubble pressure and an orange curve for the dew-point pressure. The black dot is located at the overall composition and the pressure. When two phases are present, the
diagram has a blue line for the bubble pressure and an orange curve for the dew-point pressure. The black dot is located at the overall composition and the pressure. When two phases are present, the 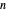 -hexane mole fractions of the liquid phase (
-hexane mole fractions of the liquid phase (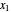 ) and the vapor phase (
) and the vapor phase ( ) are displayed. The bar graph represents the number of moles of each component in the liquid and vapor phase; purple is for
) are displayed. The bar graph represents the number of moles of each component in the liquid and vapor phase; purple is for  -hexane and green is for
-hexane and green is for 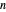 -octane.
-octane.
Contributed by: Rachael L. Baumann (February 2016)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The saturation pressures are calculated using the Antoine equation:
 ,
,
where 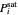 is the saturation pressure (bar) of component
is the saturation pressure (bar) of component 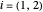 ;
; 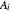 ,
, 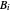 and
and 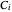 are Antoine constants; and
are Antoine constants; and 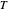 is temperature (K).
is temperature (K).
Raoult's law for a binary mixture is used to calculate the bubble 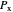 and dew
and dew 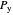 pressures:
pressures:
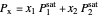 ,
,
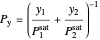 ,
,
where 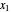 and
and 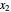 are the liquid mole fractions of each component
are the liquid mole fractions of each component 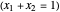 and
and 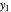 and
and 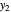 are the vapor mole fractions
are the vapor mole fractions 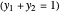 .
.
The overall mole fraction of component 1 is  , where
, where  and
and 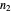 are the total moles of each component.
are the total moles of each component.
When only vapor is present,
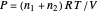 ,
,
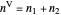 ,
,
where 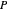 is pressure (bar),
is pressure (bar), 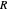 is the gas constant ([L bar]/[mol K]),
is the gas constant ([L bar]/[mol K]), 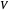 is volume (L) and
is volume (L) and 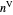 are moles of vapor.
are moles of vapor.
The following five equations are solved for 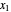 ,
, 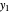 ,
, 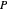 ,
, 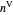 , and liquid moles
, and liquid moles 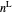 when both liquid and vapor are present.
when both liquid and vapor are present.
From Raoult's law:
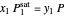 ,
,
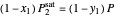 .
.
From overall and species mole balances:
 ,
,
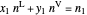 .
.
From a volume balance:
 ,
,
where 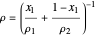 is the molar density of the mixture (mol/L).
is the molar density of the mixture (mol/L).
The screencast video at [1] explains how to use this Demonstration.
Reference
[1] Adding a Second Component to a Fixed-Volume Container [Video]. (Aug 31, 2016) www.colorado.edu/learncheme/thermodynamics/AddingSecondComponentFixedVolume.xhtml.
Permanent Citation