Addition of Points on an Elliptic Curve over the Reals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
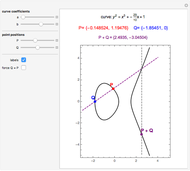
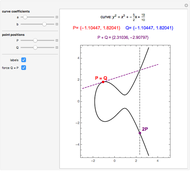
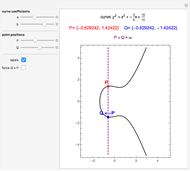
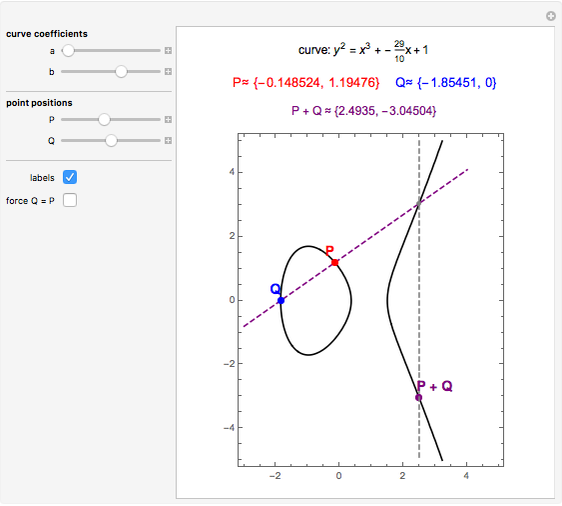
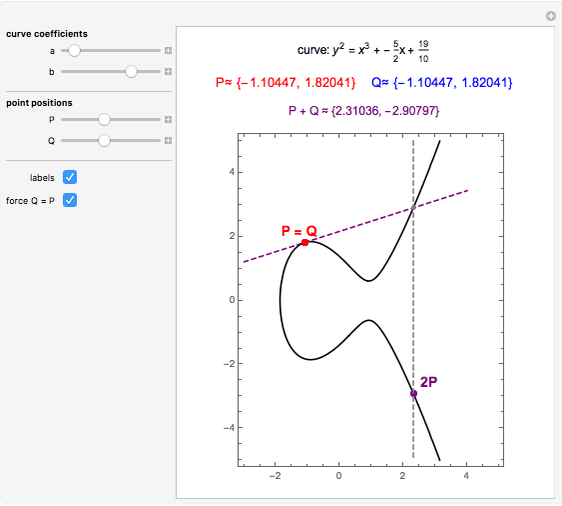
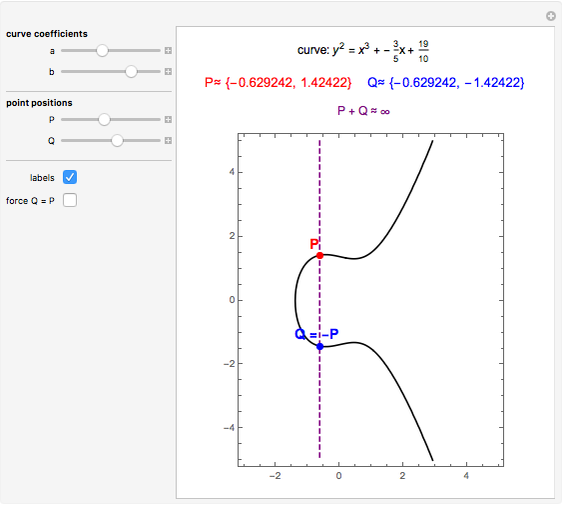
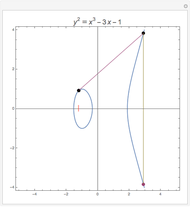
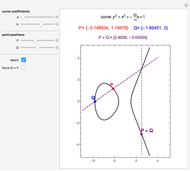
An elliptic curve over the reals forms a group under an addition law defined by line intersection and reflection. The controls allow for various elliptic curves and various points on those curves. The elliptic curve sum of the two points and the relevant lines are shown.
Contributed by: Eric Errthum (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For two points P and Q on an elliptic curve, the addition is defined as follows. Draw the line through P and Q to intersect the curve in a third point; then reflect that point in the  axis. When P = Q, use the tangent line at P. The identity of the group is ∞, the "point at infinity", which conceptually lies at the top and bottom of every vertical line. This idea can be made rigorous through projective geometry. Also, note that the curve defined by
axis. When P = Q, use the tangent line at P. The identity of the group is ∞, the "point at infinity", which conceptually lies at the top and bottom of every vertical line. This idea can be made rigorous through projective geometry. Also, note that the curve defined by 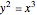 is not differentiable at (0, 0) and is thus excluded.
is not differentiable at (0, 0) and is thus excluded.
Permanent Citation
"Addition of Points on an Elliptic Curve over the Reals"
http://demonstrations.wolfram.com/AdditionOfPointsOnAnEllipticCurveOverTheReals/
Wolfram Demonstrations Project
Published: March 7 2011