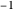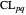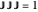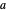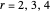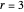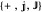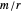Algebraic Loops (1); Properties

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
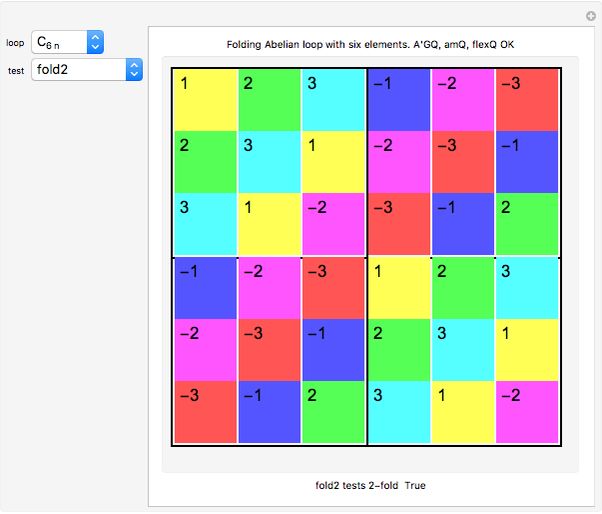
An algebraic loop (or reduced quasigroup) describes the closed binary multiplication of a set of "unsigned elements" (the product of  and
and  appears in the
appears in the 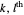 position). The companion Demonstration, Algebraic Loops (2), shows how an algebraic loop also acts as a Cayley multiplication table for unsigned vectors (ordered sets of elements such as
position). The companion Demonstration, Algebraic Loops (2), shows how an algebraic loop also acts as a Cayley multiplication table for unsigned vectors (ordered sets of elements such as  ).
).
Contributed by: Roger Beresford (March 2011)
Open content licensed under CC BY-NC-SA
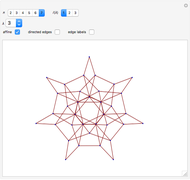
Snapshots
Details
This Demonstration only handles simple tests on small finite loops. The Demonstrations Algebraic Loops (2) and (3) investigate the algebraic properties of loops, dealing with symmetry-conserving partial-fraction vector-division "hoop algebras" with generalized signs. Hoops (which, by definition, conserve their determinants as symmetries) have the Moufang properties, ensuring that every vector has a multiplicative inverse. Later Demonstrations are concerned with the non-algebraic properties of associative and alternative tables (groups and octonions).
The GroupLoopHoop7.m package ([1], in MathSource/4894) is the source of the data, procedures, and nomenclature.  and
and 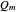 are the cyclic and quaternionic groups with
are the cyclic and quaternionic groups with 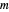 elements.
elements.  is the dihedral group with
is the dihedral group with  elements;
elements; 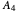 has 12 elements;
has 12 elements;  implies creation from Pauli
implies creation from Pauli  -matrices;
-matrices;  implies a non-conservative loop;
implies a non-conservative loop;  implies a non-associative Moufang loop;
implies a non-associative Moufang loop; 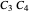 etc. are direct compositions; trailing
etc. are direct compositions; trailing  ,
,  , etc indicates isomorphs.
, etc indicates isomorphs.
The main reference for loops is
[2] J. D. H. Smith and A. B. Romanowska, Post-Modern Algebra, New York: Wiley Interscience, 1999.
Permanent Citation