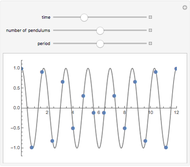
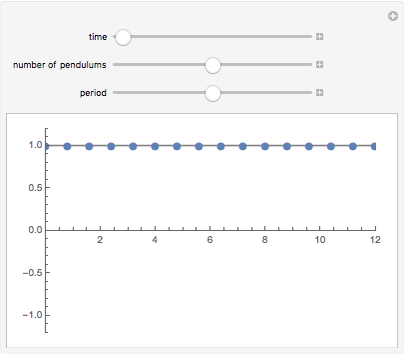
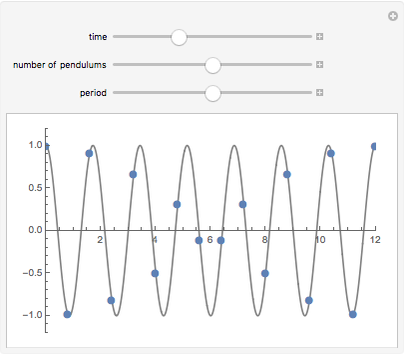
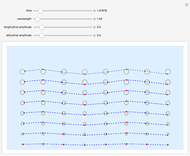
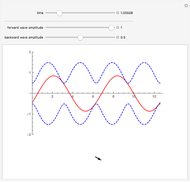
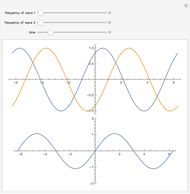
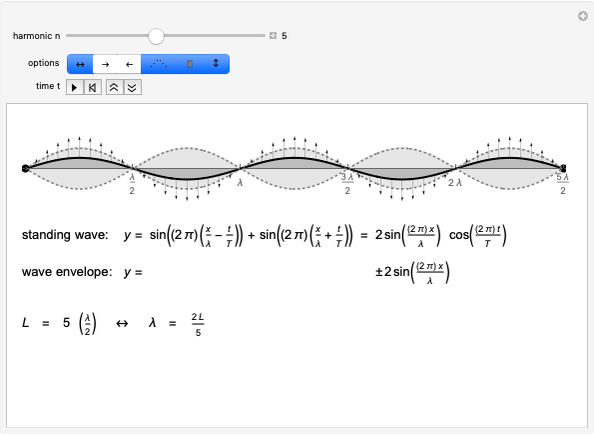
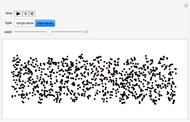
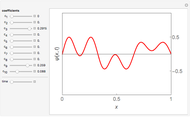
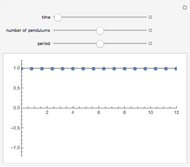
This Demonstration simulates pendulum waves with 10 to 20 uncoupled pendulums and a period of 30 to 90 seconds. The linear approximation to pendulum motion is used, so that larger angles are less accurately represented. The dots represent individual pendulums viewed from above. The light gray line plotted underneath is an approximation of the waveform. The Demonstration shows how aliasing produces the visual effects in the pendulum waves as seen in [1] and [2]. Aliasing in signal processing relates to the relationship between analog data and its approximation in digital form.