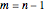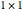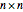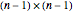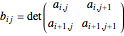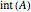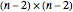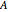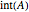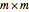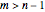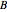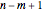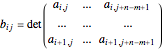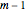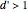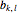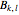Alice and Jacobi in Determinantland

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
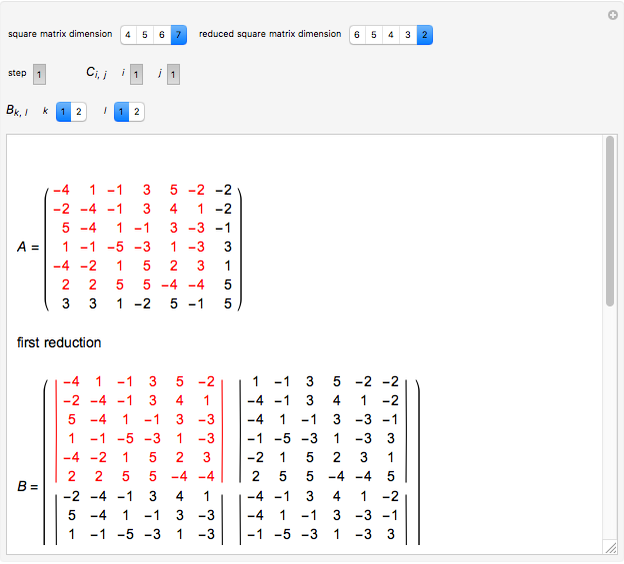
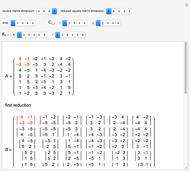
This Demonstration shows how to calculate the determinant of a generic square matrix by an alternative method to the classic Laplace expansion. The starting point is Jacobi's theorem, which condenses an 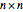 matrix into an
matrix into an  matrix, where
matrix, where 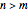 .
.
Contributed by: D. Meliga and S. Z. Lavagnino (October 2018)
Additional contributions by: F. Mandirola
Open content licensed under CC BY-NC-SA
Details
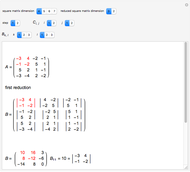
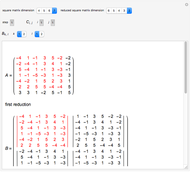
Snapshot 1: lowering the dimension by one through the determinant of several 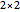 square matrices
square matrices
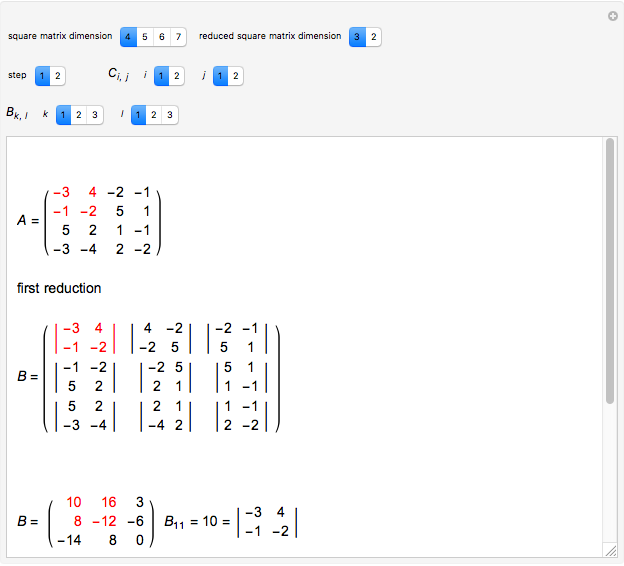
Snapshot 2: lowering the dimension from a 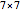 square matrix to a
square matrix to a 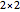 square matrix; in this case only one step is needed to find the determinant
square matrix; in this case only one step is needed to find the determinant
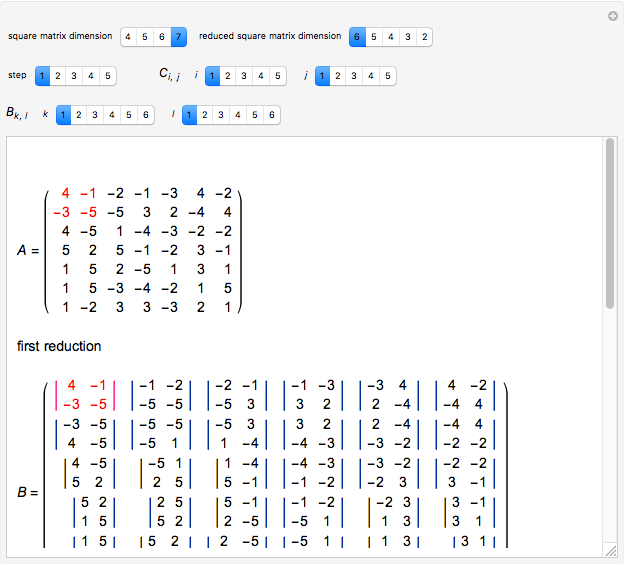
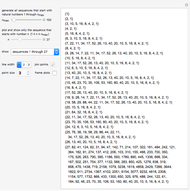
Snapshot 3: lowering the dimension from a 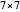 square matrix to a
square matrix to a 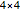 square matrix; in this case there are three steps left to find the determinant
square matrix; in this case there are three steps left to find the determinant
References
[1] D. M. Bressoud, Proofs and Confirmations: The Story of the Alternating Sign Matrix Conjecture, New York: Cambridge University Press, 1999.
[2] A. Rice and E. Torrence, "Lewis Carroll’s Condensation Method for Evaluating Determinants," Math Horizons, 14(2), 2006 pp. 12–15. (Aug 29, 2018) www.maa.org/sites/default/files/pdf/upload_library/22/Evans/Horizons-Nov06-p12-15.pdf.
Snapshots
Permanent Citation