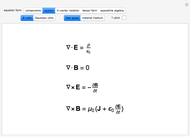
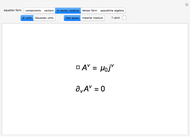
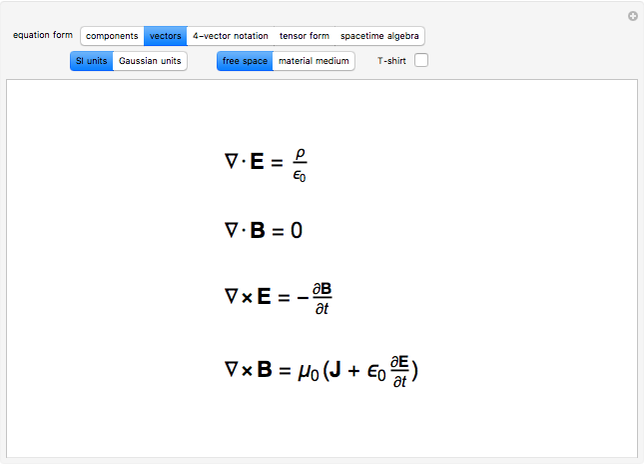
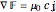Alternative Forms of Maxwell's Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
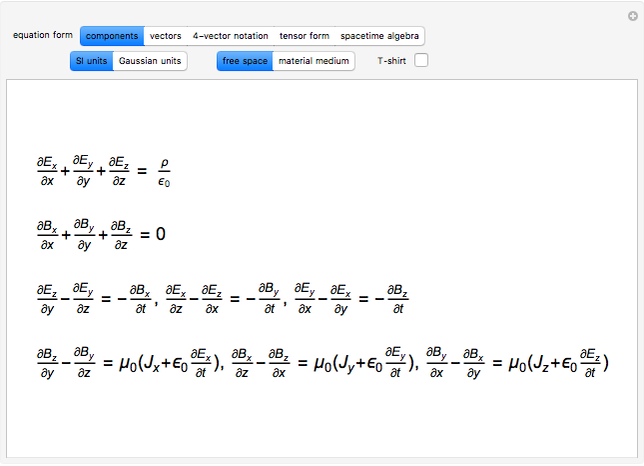
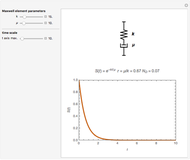
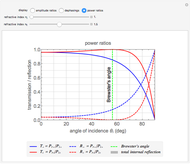
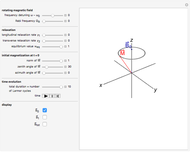
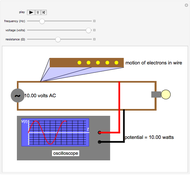
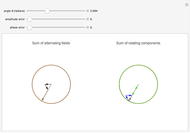
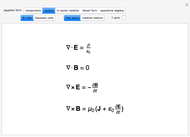
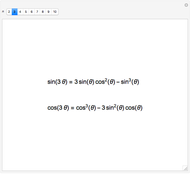
To anyone versed in science, the immense range of physical phenomena that can be encoded in Maxwell’s four relatively compact equations is breathtaking. Added to this is the remarkable symmetry between electric and magnetic variables and the fundamental underlying symmetry inherent in the special theory of relativity. One suggested measure of elegance is whether the equations can fit nicely on a T-shirt.
[more]
Contributed by: S. M. Blinder (September 2018)
Open content licensed under CC BY-NC-SA
Details
Key to symbols:
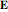 electric field,
electric field,
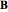 magnetic induction,
magnetic induction,
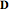 electric displacement,
electric displacement,
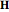 magnetic field,
magnetic field,
 charge density,
charge density,
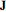 current density,
current density,
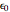 vacuum permittivity,
vacuum permittivity,
 vacuum permeability,
vacuum permeability,
 speed of light,
speed of light,
 vector potential,
vector potential,
 scalar potential,
scalar potential,
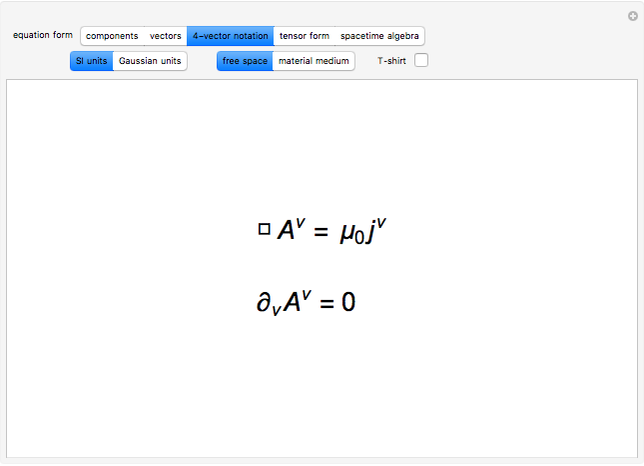
 4-potential,
4-potential,
 4-current,
4-current,
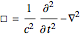 d’Alembertian operator,
d’Alembertian operator,
 ,
,
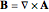 ,
,
 electromagnetic field tensor,
electromagnetic field tensor,
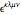 Levi–Civita symbol.
Levi–Civita symbol.
In spacetime algebra:
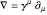 ,
,
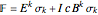 ,
,
 .
.
References
[1] Wikipedia. "Maxwell's Equations." (Aug 27, 2018) en.wikipedia.org/wiki/Maxwell%27 s_equations.
[2] Wikipedia. "Electromagnetic Four-Potential." (Aug 27, 2018) en.wikipedia.org/wiki/Electromagnetic_four-potential.
[3] Wikipedia. "Covariant Formulation of Classical Electromagnetism." (Aug 27, 2018) en.wikipedia.org/wiki/Covariant_formulation_of _classical _electromagnetism.
[4] Wikipedia. "Mathematical Descriptions of the Electromagnetic Field." (Aug 27, 2018) en.wikipedia.org/wiki/Mathematical_descriptions_of _the _electromagnetic _field.
Snapshots
Permanent Citation