Altitude of a Tetrahedron Given Its Edges

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
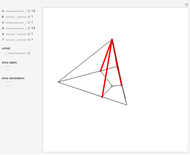
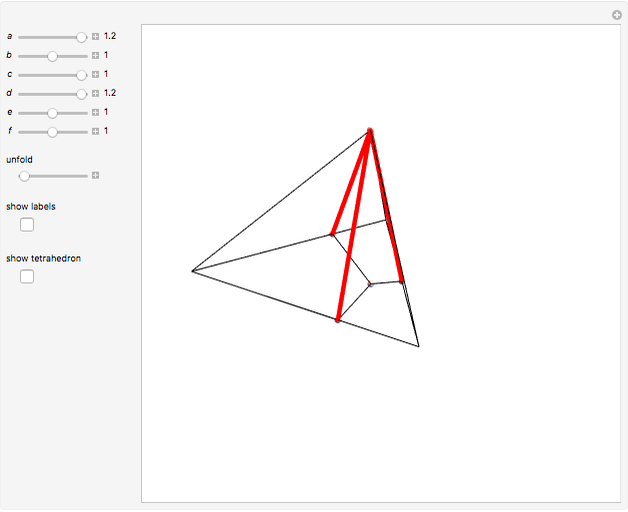
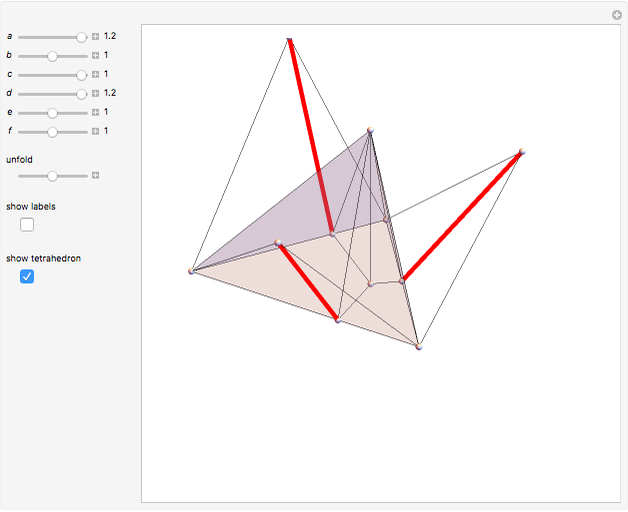
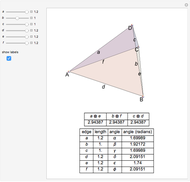
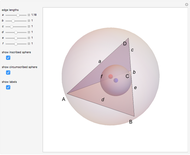
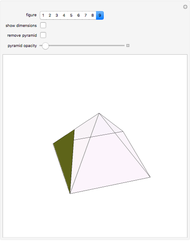
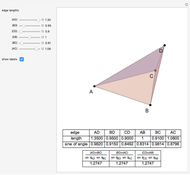
This Demonstration constructs an altitude of a tetrahedron  given its edge lengths
given its edge lengths  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . (In the figure, the edge length of
. (In the figure, the edge length of  is
is  .) Suppose the altitude is from vertex
.) Suppose the altitude is from vertex  to the opposite face
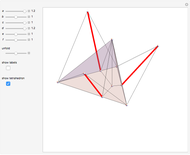
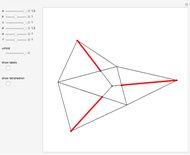
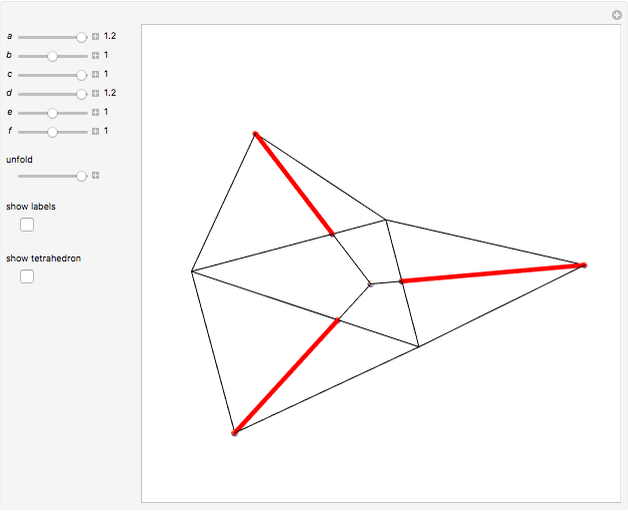
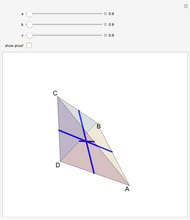
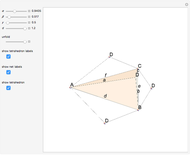
to the opposite face  . First, construct the net of
. First, construct the net of  with the triangle
with the triangle  in the center (unfold completely). Normals from the vertex
in the center (unfold completely). Normals from the vertex  to the sides
to the sides  ,
,  ,
,  meet at a point
meet at a point  . This is the 3D orthogonal projection of vertex
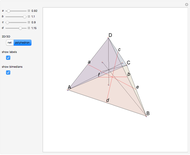
. This is the 3D orthogonal projection of vertex  . In 3D, the lines
. In 3D, the lines  ,
,  and the altitude form a right triangle with
and the altitude form a right triangle with  as its hypotenuse. So we can construct the altitude as a leg of the triangle.
as its hypotenuse. So we can construct the altitude as a leg of the triangle.
Contributed by: Izidor Hafner (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Altitude of a Tetrahedron Given Its Edges"
http://demonstrations.wolfram.com/AltitudeOfATetrahedronGivenItsEdges/
Wolfram Demonstrations Project
Published: March 27 2017