American Capped Call Options with Exponential Cap

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
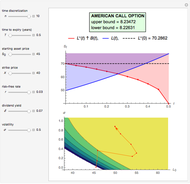
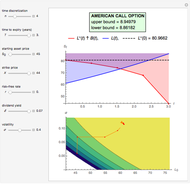
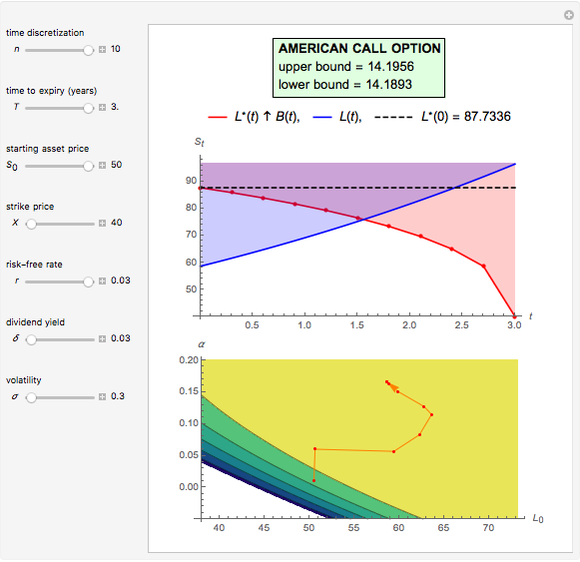
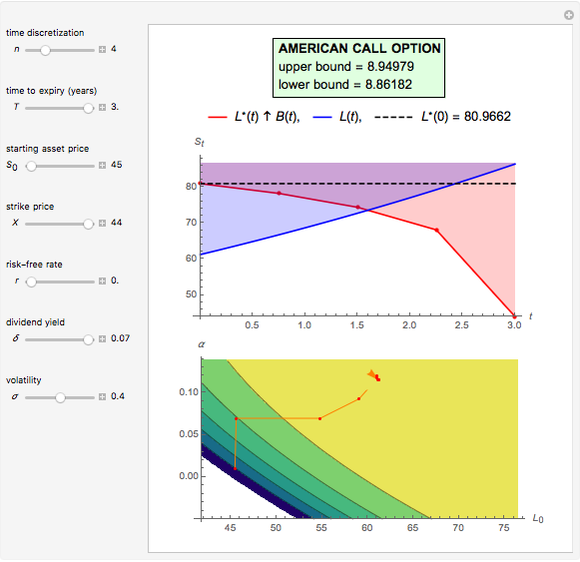
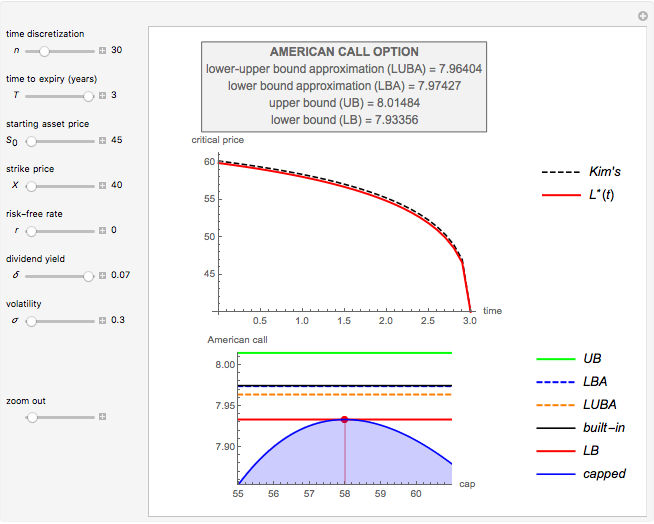
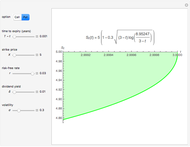
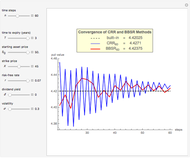
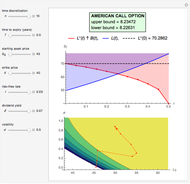
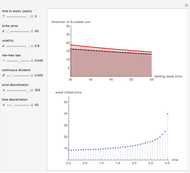
This Demonstration shows the maximization process of an American capped call option with an exponential cap (or barrier) [4]. Because the capped call must be instantly exercised if the underlying asset price rises above a price, determined by an exponential function over time,  , where
, where 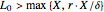 and
and 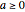 , its value never exceeds the value of the standard American call. Thus, identifying the parameters
, its value never exceeds the value of the standard American call. Thus, identifying the parameters 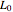 and
and  that maximize the capped call payoff function
that maximize the capped call payoff function 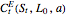 , we obtain a lower bound for the American call price
, we obtain a lower bound for the American call price 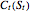 . Moreover, the evaluation of the capped call payoff function partial derivatives with respect to the cap parameters
. Moreover, the evaluation of the capped call payoff function partial derivatives with respect to the cap parameters 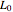 and
and  , while the underlying asset price approaches
, while the underlying asset price approaches 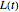 from below, provides a lower approach
from below, provides a lower approach 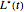 for the American call optimal exercise boundary
for the American call optimal exercise boundary 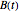 . Finally, after replacing
. Finally, after replacing 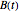 with
with 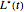 in Kim's integral equation [1], an upper bound for the American call price is obtained. Thus the capped call option is really a tool used to bracket the pricing of the commonly traded American option.
in Kim's integral equation [1], an upper bound for the American call price is obtained. Thus the capped call option is really a tool used to bracket the pricing of the commonly traded American option.
Contributed by: Michail Bozoudis (February 2016)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
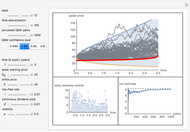
Snapshots
Details
M. Broadie and J. Detemple [2] specified a three-step procedure for valuing American capped call options when the cap is described by the function 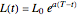 . Based on this procedure, S.-L. Chung, M.-W. Hung, and J.-Y. Wang [4] approximated an American call payoff
. Based on this procedure, S.-L. Chung, M.-W. Hung, and J.-Y. Wang [4] approximated an American call payoff 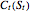 by maximizing the value of a call with exponential cap written on the same asset. If the price of the underlying asset is
by maximizing the value of a call with exponential cap written on the same asset. If the price of the underlying asset is  when
when 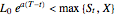 , the payoff of the capped call option is
, the payoff of the capped call option is 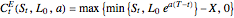 , where
, where 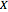 is the strike price and
is the strike price and 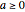 is the cap's constant growth rate. The payoff is the same as a standard American option, except that the cap function
is the cap's constant growth rate. The payoff is the same as a standard American option, except that the cap function 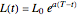 limits the maximum possible payoff. Since the policy of exercising when the asset price reaches the exponential cap
limits the maximum possible payoff. Since the policy of exercising when the asset price reaches the exponential cap 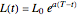 is an admissible policy for the American option,
is an admissible policy for the American option, 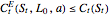 for any
for any 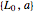 .
.
Hence a lower bound 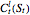 is still obtained after optimizing over
is still obtained after optimizing over 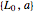 . Denote the optimal solution
. Denote the optimal solution 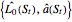 as
as
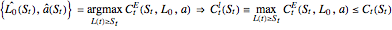 .
.
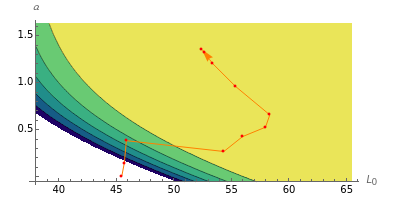
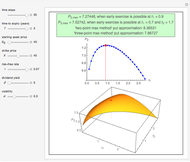
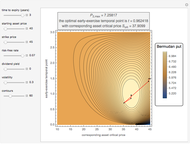
The determination of  is a bivariate differentiable optimization problem for any given
is a bivariate differentiable optimization problem for any given  . With the formulas of derivatives
. With the formulas of derivatives 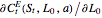 and
and 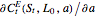 , the optimal solution should satisfy
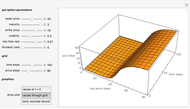
, the optimal solution should satisfy 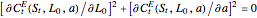 . In this Demonstration, Mathematica's built-in function FindMaximum is applied to maximize the payoff function
. In this Demonstration, Mathematica's built-in function FindMaximum is applied to maximize the payoff function 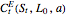 and determine the optimal solution
and determine the optimal solution 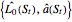 .
.
Following the same idea of M. Broadie and J. Detemple [3], the evaluation of the capped call payoff function derivatives with respect to 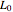 and
and  , while the underlying asset price
, while the underlying asset price  approaches
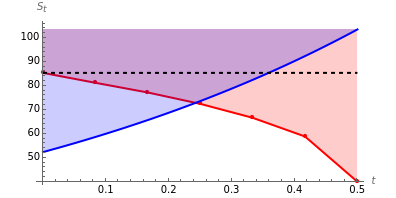
approaches 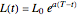 from below, leads to an exercise boundary
from below, leads to an exercise boundary  , where
, where 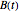 is the American call optimal early exercise boundary at time
is the American call optimal early exercise boundary at time  . The boundary
. The boundary 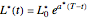 is the solution to the equation
is the solution to the equation
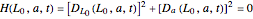 ,
,
where 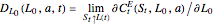 and
and 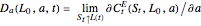 .
.
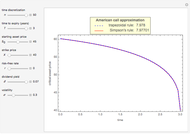
In this Demonstration, Mathematica's built-in function FindMinimum is applied to minimize 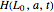 . Following the method of M. Broadie and J. Detemple [3], an upper bound for the American call price is obtained after replacing the optimal early exercise boundary function
. Following the method of M. Broadie and J. Detemple [3], an upper bound for the American call price is obtained after replacing the optimal early exercise boundary function 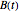 with
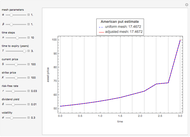
with 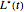 in Kim's integral equation [1]. The integral in Kim's equation represents the early exercise premium and is approximated by Simpson's rule.
in Kim's integral equation [1]. The integral in Kim's equation represents the early exercise premium and is approximated by Simpson's rule.
Compared to the method that uses a constant cap over time [3], the method with the exponential cap function [4] leads to tighter bounds for the theoretical American call price.
References
[1] I. J. Kim, "The Analytic Valuation of American Options," The Review of Financial Studies, 3(4), 1990 pp. 547–572.
[2] M. Broadie and J. Detemple, "American Capped Call Options on Dividend-Paying Assets," The Review of Financial Studies, 8(1), 1995 pp. 161–191.
[3] M. Broadie and J. Detemple, "American Option Valuation: New Bounds, Approximations, and a Comparison of Existing Methods," The Review of Financial Studies, 9(4), 1996 pp. 1211–1250.
[4] S.-L. Chung, M.-W. Hung, and J.-Y. Wang, "Tight Bounds on American Option Prices," Journal of Banking and Finance, 34(1), 2010 pp. 77–89.
Permanent Citation