American Options on Assets with Dividends Near Expiry

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
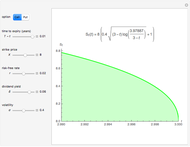
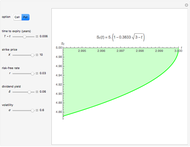
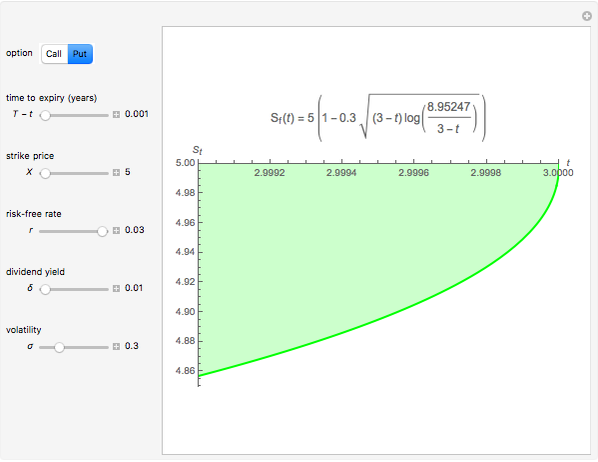
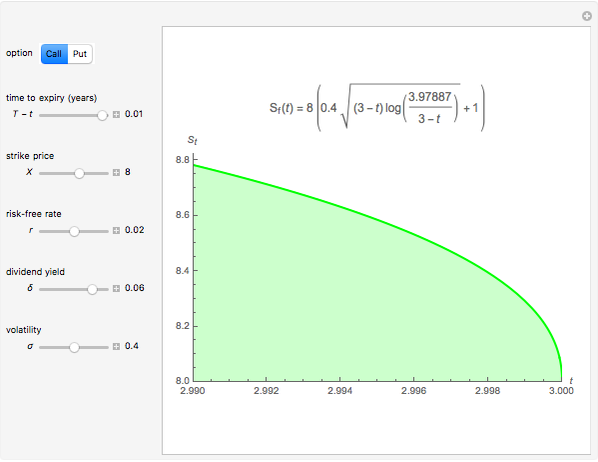
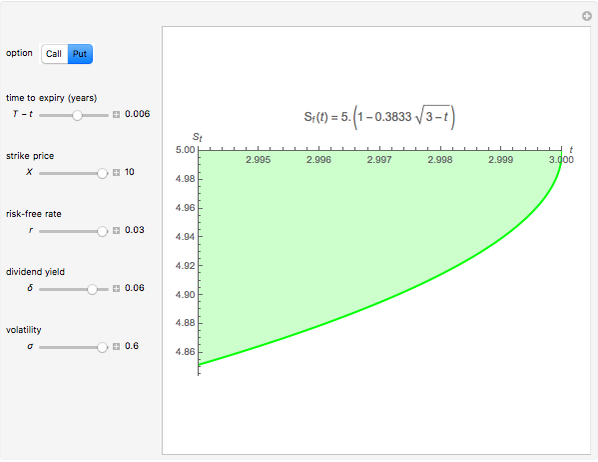
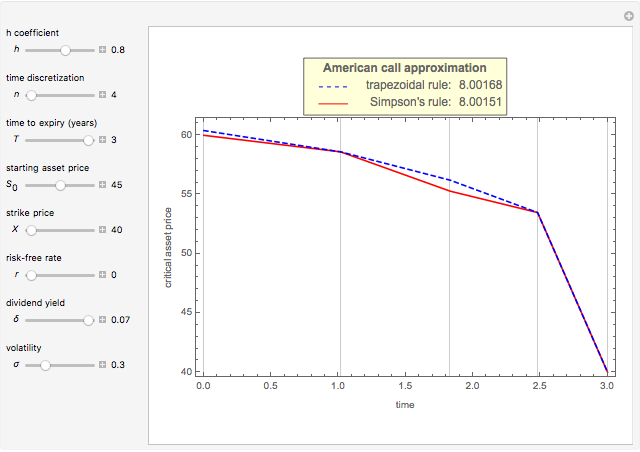
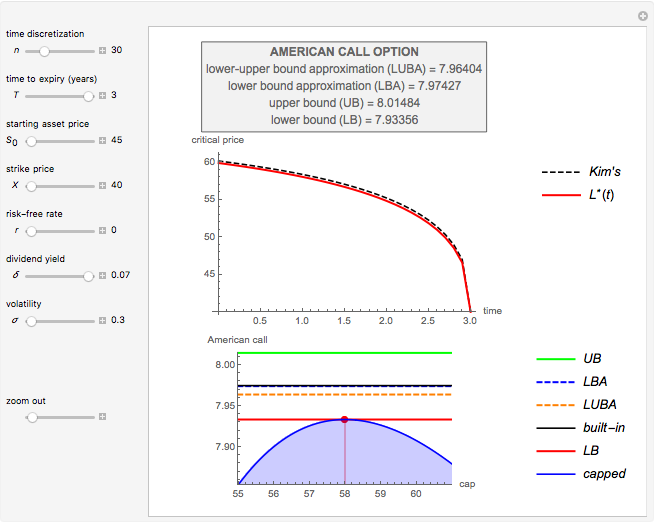
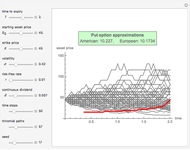
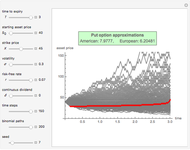
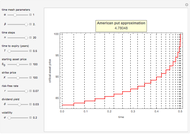
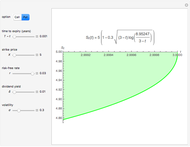
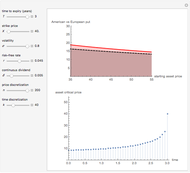
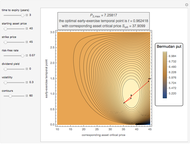
This Demonstration shows an explicit expression for the optimal exercise boundary of American options on assets with dividends. The function 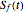 of the optimal exercise boundary is only valid near expiry. The graph shows the
of the optimal exercise boundary is only valid near expiry. The graph shows the 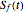 curve (green line) near expiry for a three-year maturity option. For the option's holder, it is not optimal to exercise the option while the asset price
curve (green line) near expiry for a three-year maturity option. For the option's holder, it is not optimal to exercise the option while the asset price 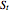 moves within the colored area.
moves within the colored area.
Contributed by: Michail Bozoudis (March 2016)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
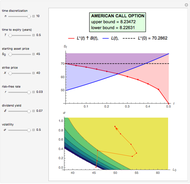
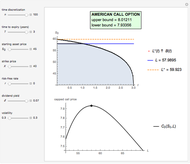
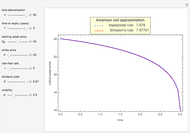
Snapshots
Details
J. D. Evans, R. Kuske, and J. B. Keller [1] provide explicit expressions valid near expiry (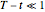 ) for the optimal exercise boundary of American put and call options on assets with dividends. The results depend sensitively on the ratio of the dividend yield rate
) for the optimal exercise boundary of American put and call options on assets with dividends. The results depend sensitively on the ratio of the dividend yield rate  to the interest rate
to the interest rate  .
.
The optimal exercise boundary is singular at expiry, and its behavior is a classical problem of mathematical finance. The nature of these singularities cannot be determined by numerical calculation. Due to the behavior of the optimal exercise boundary near expiry, it is more difficult to retain accuracy in approximating the boundary using numerical methods and other types of approximations. These inaccuracies become more significant when pricing these options in the period close to expiry. In both lattice methods and the projected successive over-relaxation (SOR) method for partial differential equations (PDE), a fine discretization must be used near expiry, and this is both expensive and limited in accuracy. Therefore, the explicit expression near expiry can be combined with the numerical methods to calculate the optimal exercise boundary away from expiry.
The analytic expressions are derived twice: once by solving an integral equation and again by constructing matched asymptotic expansions. For 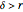 the put boundary near expiry tends parabolically to the value
the put boundary near expiry tends parabolically to the value 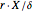 , where
, where 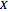 is the strike price, while for
is the strike price, while for 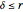 the boundary tends to
the boundary tends to 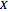 in the parabolic-logarithmic form:
in the parabolic-logarithmic form:
• 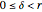 ,
, 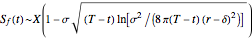 ,
,
•  ,
, 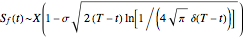 ,
,
• 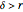 ,
, 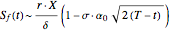 , where
, where 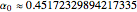 .
.
Analogous results for the optimal exercise boundary of an American call option on an asset with dividends are:
• 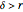 ,
, 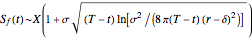 ,
,
•  ,
, 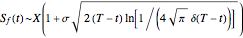 ,
,
• 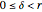 ,
, 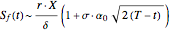 .
.
Reference
[1] J. D. Evans, R. Kuske, and J. B. Keller, “American Options on Assets with Dividends Near Expiry,” Mathematical Finance, 12(3), 2002 pp. 219–237. doi:10.1111/1467-9965.02008.
Permanent Citation