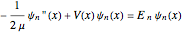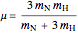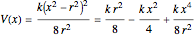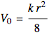Ammonia Inversion: Classical and Quantum Models

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
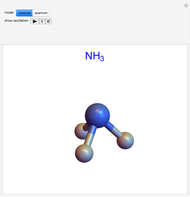
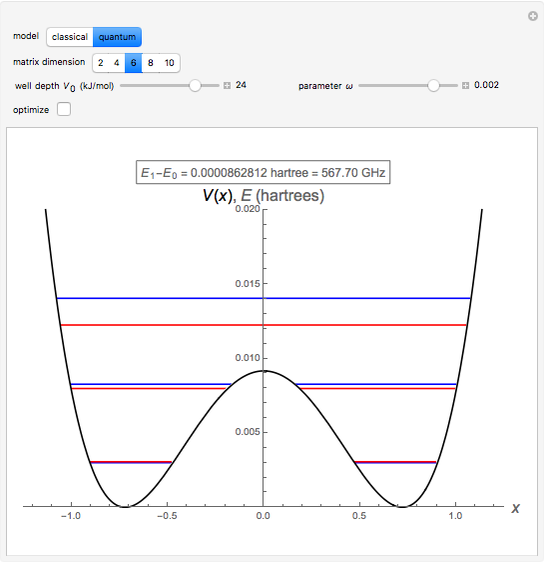
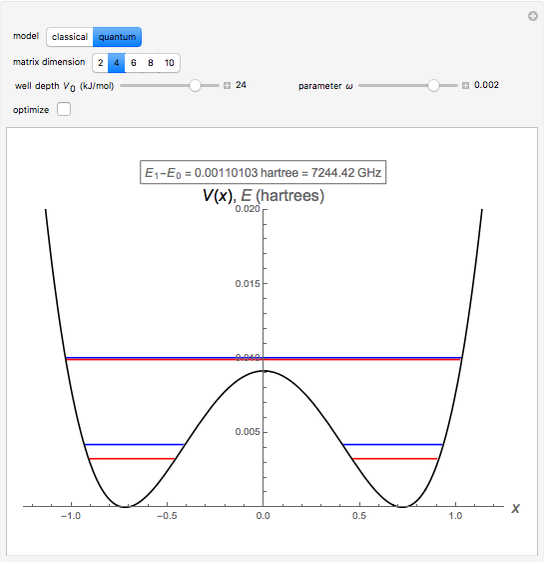
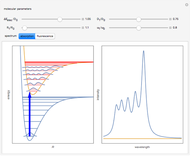
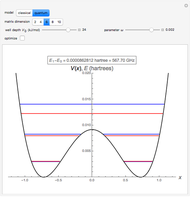
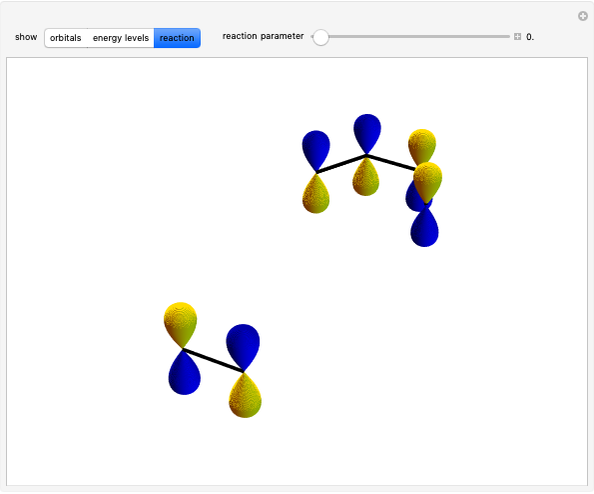
The ammonia molecule  has a trigonal pyramidal configuration, with the nitrogen atom connected to three hydrogen atoms. The molecule readily undergoes inversion at room temperature, like an umbrella turning itself inside out in a strong wind. The energy barrier to this inversion is 24.2 kJ/mol. A resonance frequency of 24.87 GHz, in the microwave region, corresponds to the energy splitting of the two lowest vibrational levels. This transition is exploited in the ammonia maser.
has a trigonal pyramidal configuration, with the nitrogen atom connected to three hydrogen atoms. The molecule readily undergoes inversion at room temperature, like an umbrella turning itself inside out in a strong wind. The energy barrier to this inversion is 24.2 kJ/mol. A resonance frequency of 24.87 GHz, in the microwave region, corresponds to the energy splitting of the two lowest vibrational levels. This transition is exploited in the ammonia maser.
Contributed by: S. M. Blinder (February 2019)
Open content licensed under CC BY-NC-SA
Details
The ladder operators can be defined by
 ,
,
 ,
,
with an adjustable parameter  introduced. The nonvanishing matrix elements of the Hamiltonian can then be computed, giving
introduced. The nonvanishing matrix elements of the Hamiltonian can then be computed, giving
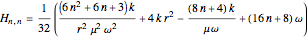 ,
,
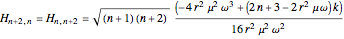 ,
,
 .
.
The eigenvalues are then determined using the Eigenvalue routine for selected dimensions 2 to 10.
Reference
[1] S. M. Blinder, "Ammonia Inversion Energy Levels Using Operator Algebra." arxiv.org/abs/1809.08178.
Snapshots
Permanent Citation