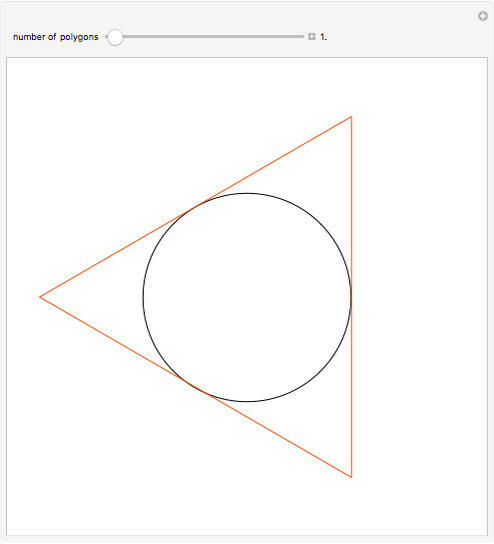
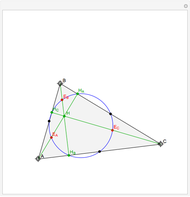
An Illustration of the Central Limit Theorem Using Chi-Square Samples

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
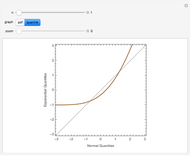
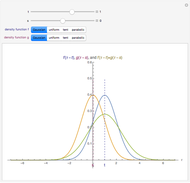
If 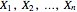 is a random sample from a distribution with finite mean
is a random sample from a distribution with finite mean  and variance
and variance  , then the central limit theorem asserts that the density function of
, then the central limit theorem asserts that the density function of 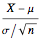 approaches a standard normal density as
approaches a standard normal density as  . If the underlying distribution is a
. If the underlying distribution is a 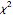 distribution with one degree of freedom, the density function of
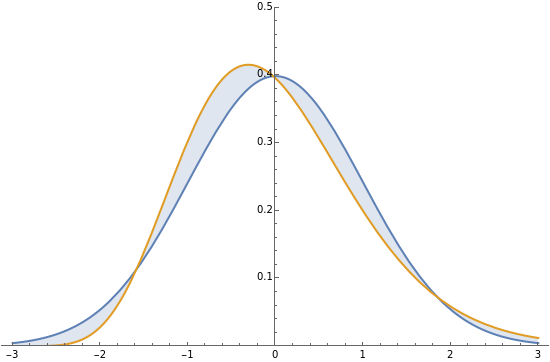
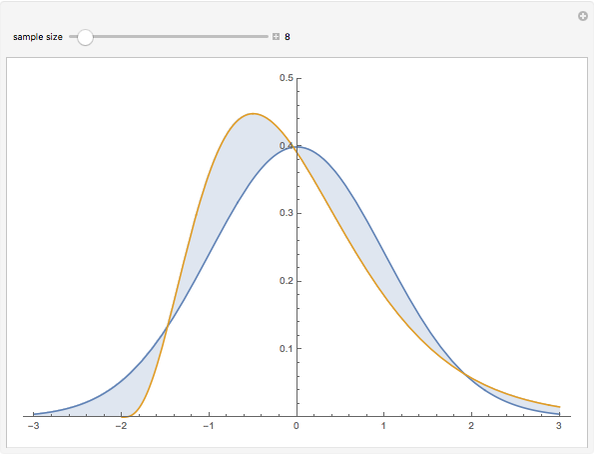
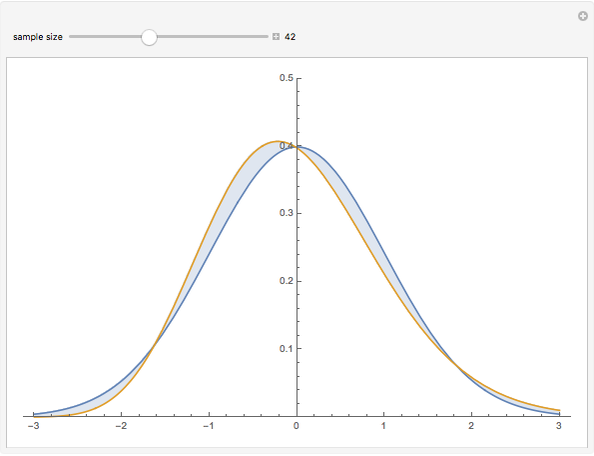
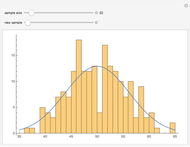
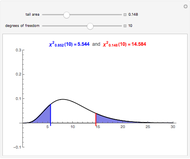
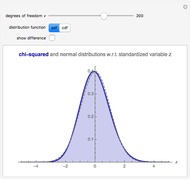
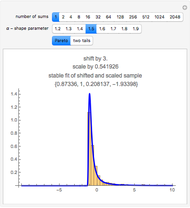
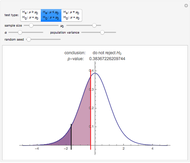
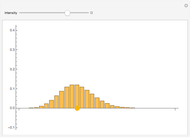
distribution with one degree of freedom, the density function of 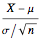 can be derived exactly (see the details). This Demonstration compares that density (purple) with a standard normal density (blue) for various values of
can be derived exactly (see the details). This Demonstration compares that density (purple) with a standard normal density (blue) for various values of  .
.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
If 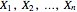 is a random sample from a
is a random sample from a 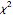 distribution with one degree of freedom and
distribution with one degree of freedom and 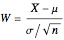 , the density function of
, the density function of 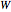 is
is 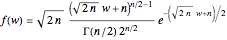 .
.
Permanent Citation