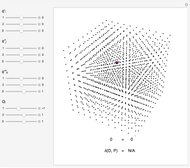
Analysis of Lattice Vibrations in Two Dimensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
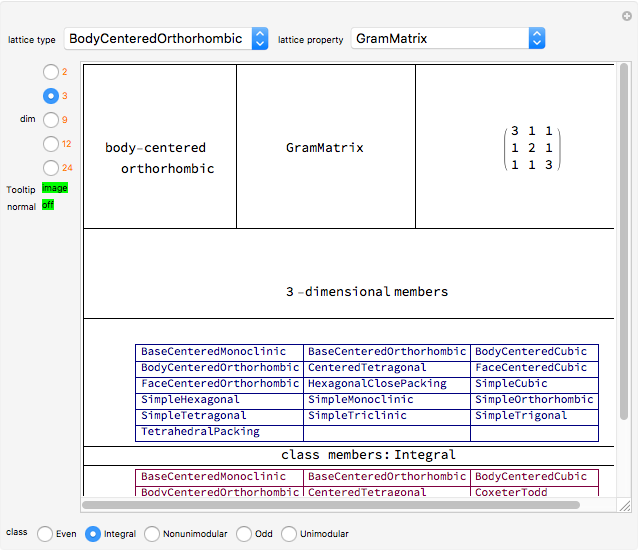
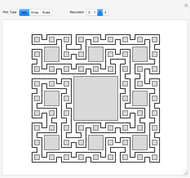
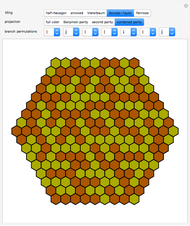
At first glance, the hexagonal and square lattices appear to have the same symmetry as their unit cells (a simple hexagon or square), but closer examination reveals more rotational and reflectional symmetries, not to mention a countably infinite number of translations. Of course, a real crystal lattice deviates from perfect symmetry as it interacts with photons in energy transfer that results in the creation of discrete vibrational states.
[more]
Contributed by: Brad Klee (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
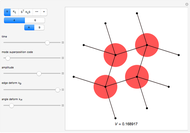
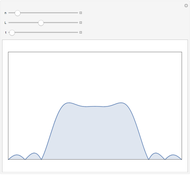
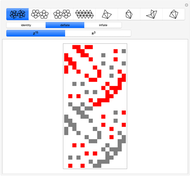
Snapshot 1, Energy Summation Unit: As a tile in the lattice deforms according to the propagation of a wavefunction away from the equilibrium configuration, the potential energy of the entire tiling increases because of the deformed edges and angles. Each contribution to the increase in potential energy is shown as a highlighted edge or highlighted vertex, and the magnitude of the highlighted region indicates the contribution of that deformation to the total potential energy.
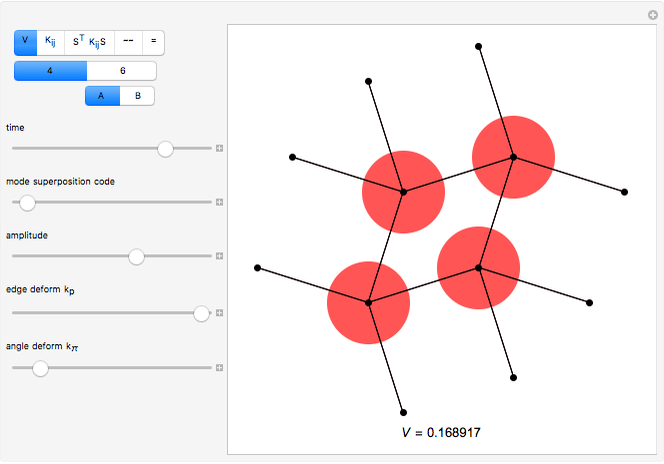
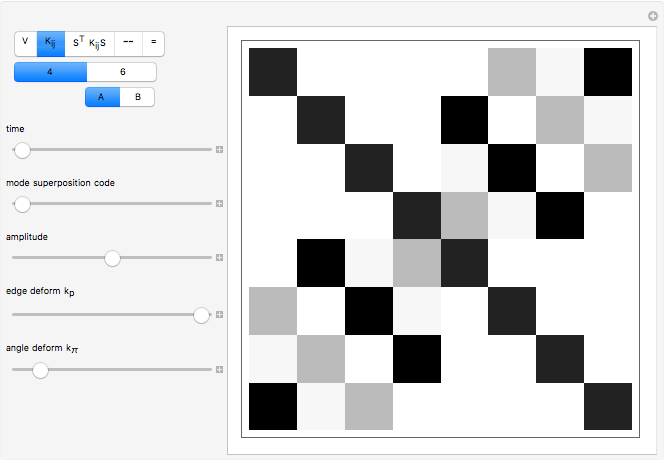
Snapshot 2, Hessian Matrix: An array plot of the Hessian matrix shows the magnitude of the second derivative of the potential energy, which is computed using a central difference method and two perturbations for each atom. The eigenvectors and eigenvalues of this matrix are the normal modes and their corresponding vibrational frequencies. The Hessian matrix, given by 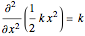 , has the units of a force constant.
, has the units of a force constant.
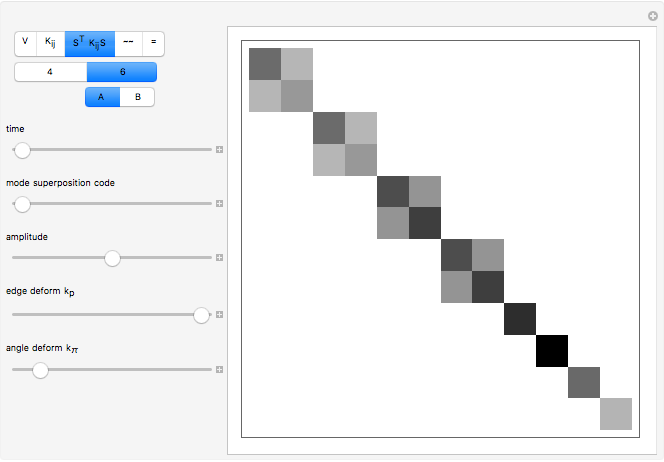
Snapshot 3, Block Diagonal Transformation: The perturbation basis elements transform into one another according to the operations of dihedral symmetry, for both square and hexagonal lattices. The Hessian matrix computed from these perturbations does not change under conjugation by any transformation of the dihedral group, that is, 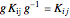 . Thus,
. Thus, 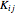 can be reduced to block diagonal form using a transformation
can be reduced to block diagonal form using a transformation 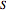 derived from the irreducible representations of the dihedral group. Eigenvectors computed from the block-diagonalized matrix can all be real even if eigenvectors computed from the untransformed matrix are complex.
derived from the irreducible representations of the dihedral group. Eigenvectors computed from the block-diagonalized matrix can all be real even if eigenvectors computed from the untransformed matrix are complex.
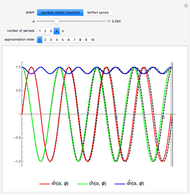
Snapshot 4, Energy Level Diagram: This plot shows energy levels for each selected wavefunction. The left-hand side of each level is labeled by some number linearly proportional to a frequency, computed from the square root of an eigenvalue of the Hessian matrix 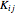 . Indices on the right-hand side correspond to symmetries of the vibrational modes, which can be determined using sets of simple linear functionals.
. Indices on the right-hand side correspond to symmetries of the vibrational modes, which can be determined using sets of simple linear functionals.
The construction of the Hessian matrix is adapted from [1]. Each angular dimension resists deformation with a factor of 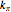 , and each linear dimension resists deformation with a factor of
, and each linear dimension resists deformation with a factor of  . The total energy of a lattice acted upon by periodic deformations is infinite and thus incalculable. However, an adequately apportioned fraction of the total energy can be computed by summing the energy from each tile multiplied by the population percentage of that tile. Care must be taken not to count edges twice.
. The total energy of a lattice acted upon by periodic deformations is infinite and thus incalculable. However, an adequately apportioned fraction of the total energy can be computed by summing the energy from each tile multiplied by the population percentage of that tile. Care must be taken not to count edges twice.
In this notebook, the energy computation is correct for the square lattice and for the A hexagonal lattice but not for the B hexagonal lattice. The A hexagonal lattice contains only three species of tiles, while the B hexagonal lattice contains 24 species of tiles. A correct computation for the B hexagonal lattice in 12 dimensions could be accomplished by changing the energy function to sum over the six edges and six angles of all 24 species, with the appropriate prefactors according to relative population and overlap of edges. Each basis pattern has a unique spectrum and perturbation periodicity. It is unknown how many basis patterns exist, and the existence or absence of a basis pattern containing 720 tiles is unproven but not excluded.
Block diagonalization is performed by considering the irreducible representations of the appropriate dihedral group. Block membership determines an important equivalency class for eigenvectors, related to selection rules and transition probabilities. A classification system based on annihilators and orthogonal to block membership has been used to number the degeneracies.
This Demonstration should not be considered physical, but systems of springs and masses can give insight for problems where restoring forces hold atoms in a specific geometric pattern while some energy excitations attempt to move them, thus creating phonons.
Thanks to Janette Dunn for providing educational resources regarding representation-derived bases.
Reference
[1] D. E. Weeks and W. G. Harter, "Rotation-Vibration Spectra of Icosahedral Molecules. II. Icosahedral Symmetry, Vibrational Eigenfrequencies, and Normal Modes of Buckminsterfullerene," Journal of Chemical Physics, 90(9), 1989 pp. 4744–4771. doi: 10.1063/1.456571.
Permanent Citation