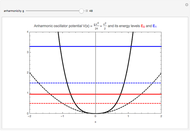
Anharmonic Oscillator Spectrum via Diagonalization of Amplitudes
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
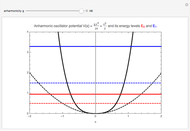
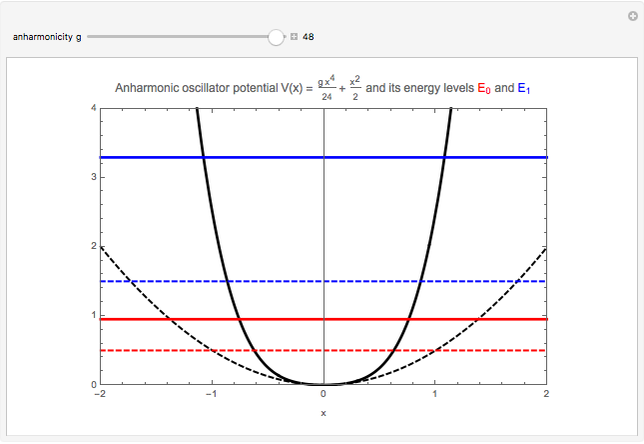
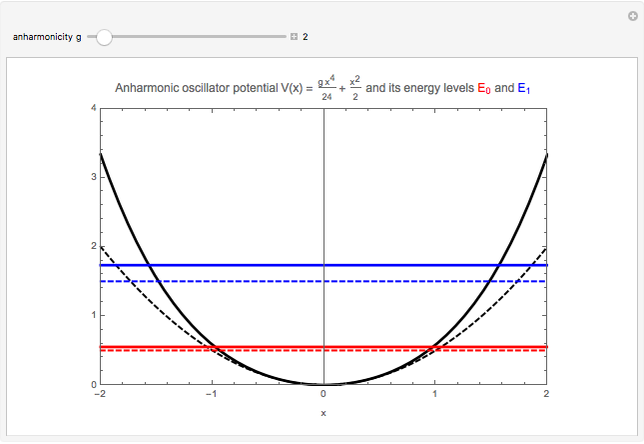
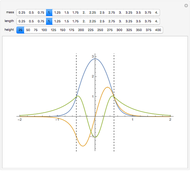
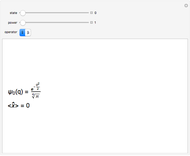
The energy spectrum of a quantum system can be accurately calculated by the numerical diagonalization of the space-discretized matrix of its evolution operator, that is, the matrix of its transition amplitudes. Here we calculate the spectrum of a one-dimensional anharmonic oscillator with the potential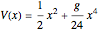 
, using level 
effective action. For a general quantum system described by the Hamiltonian 
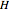, the probability for a transition from an initial state 
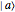to a final state 
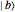in time 
is calculated as 
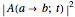, with the transition amplitude 
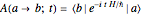. In a recently developed effective action approach, the amplitude is expressed in terms of the effective potential. Then a set of recursive relations allows systematic analytic derivation of terms in the expansion of the effective potential in the time 
. The effective action thus obtained is characterized by a chosen level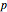 
corresponding to the maximal order 
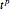occurring in its expansion.
Contributed by: Antun Balaz (March 2011)
After work by: Antun Balaz, Ivana Vidanovic, Aleksandar Bogojevic, Aleksandar Belic, and Axel Pelster
Open content licensed under CC BY-NC-SA
Snapshots
Details
The effective action approach was originally developed in a series of papers:
[1] A. Bogojevic, A. Balaz, and A. Belic, "Systematically Accelerated Convergence of Path Integrals," Phys. Rev. Lett., 94(18), 2005.
[2] A. Bogojevic, A. Balaz, and A. Belic, "Systematic Speedup of Path Integrals of a Generic N-Fold Discretized Theory," Phys. Rev. B, 72(6), 2005.
[3] A. Bogojevic, A. Balaz, and A. Belic, "Generalization of Euler's Summation Formula to Path Integrals," Phys. Lett. A, 344(2–4), 2005 pp. 84–90.
The extension of the approach to many-body systems is presented in the following papers:
[4] A. Bogojevic, I. Vidanovic, A. Balaz, and A. Belic, "Fast Convergence of Path Integrals for Many-Body Systems," Phys. Lett. A, 372(19), 2008 pp. 3341–3349.
[5] A. Balaz, A. Bogojevic, I. Vidanovic, and A. Pelster, "Recursive Schrödinger Equation Approach to Faster Converging Path Integrals," Phys. Rev. E, 79(3), 2009.
This method has been successfully applied to numerical studies of properties of various quantum systems:
[6] I. Vidanovic, A. Bogojevic, and A. Belic, "Properties of Quantum Systems via Diagonalization of Transition Amplitudes I: Discretization Effects," Phys. Rev. E, 80(6), 2009.
[7] I. Vidanovic, A. Bogojevic, A. Balaz, and A. Belic, "Properties of Quantum Systems via Diagonalization of Transition Amplitudes II: Systematic Improvements of Short-Time Propagation," Phys. Rev. E, 80(6), 2009.
Recently, this approach has been extended to systems in time-dependent potentials:
[8] A. Balaz, I. Vidanovic, A. Bogojevic, and A. Pelster, "Fast Converging Path Integrals for Time-Dependent Potentials," arXiv, 2009.
Mathematica programs developed for symbolic derivation of higher-order effective actions, as well as the C programs developed and used in numerical simulations in the above papers, can be found at http://www.scl.rs/speedup.
All programs were developed at the Scientific Computing Laboratory of the Institute of Physics — Belgrade.
Short-Time Expansion of Quantum Amplitudes
Antun Balaz
Short-Time Expansion of Amplitudes for Time-Dependent Potentials
Antun Balaz
Anharmonic Oscillator Phase Space Trajectories 2D
Michael Trott
Energy Spectrum for a Finite Potential Well
Adam Strzebonski
Temperature-Dependent Rotational Energy Spectrum
Porscha McRobbie and Eitan Geva
Harmonic Oscillator Wavefunctions
Richard Gass
Rotational-Vibrational Spectrum of a Diatomic Molecule
Porscha McRobbie and Eitan Geva
Three-Dimensional Isotropic Harmonic Oscillator
S. M. Blinder
Causal Interpretation of the Quantum Harmonic Oscillator
Klaus von Bloh
Ladder Operators for the Harmonic Oscillator
S. M. Blinder
