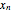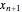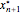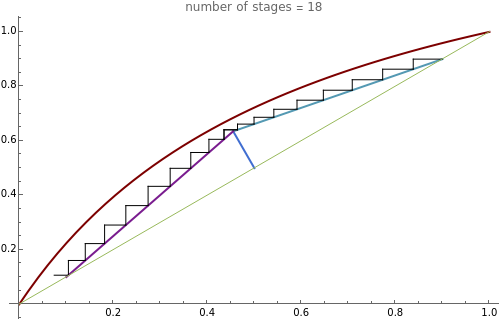
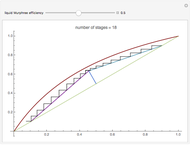
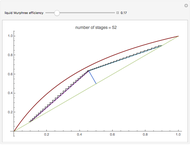
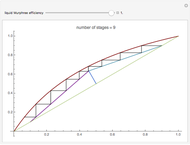
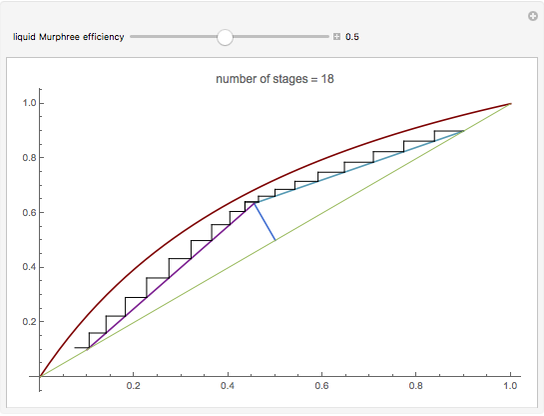
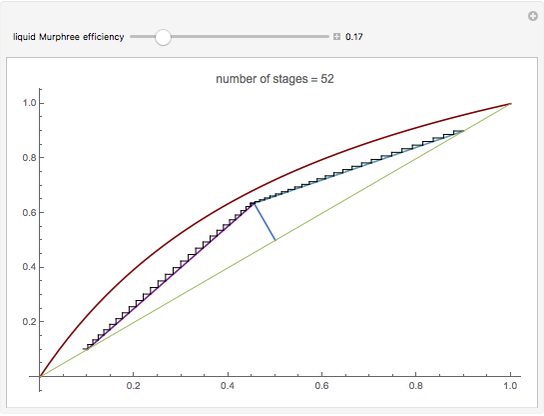
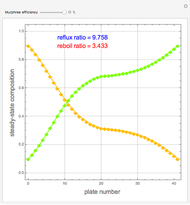
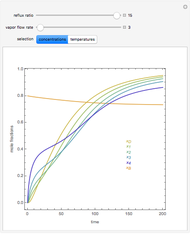
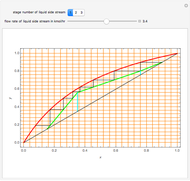
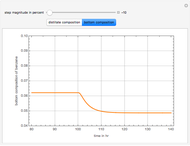
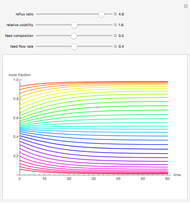
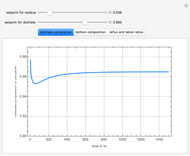
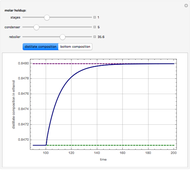
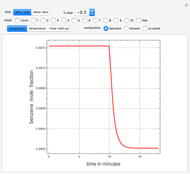
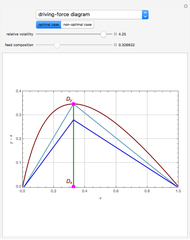
This Demonstration presents the application of the Murphree liquid efficiency method to the distillation of a binary mixture. First, the rectifying and stripping operating lines are plotted using a reflux ratio equal to 1.5 times the minimum reflux ratio. These lines are derived by writing global and partial material balances around different sections of the column. The feed line is also plotted. If the construction is correct, these three lines must intersect at the same point. Separation parameters are chosen as follows: (1) feed quality is equal to 0.75; (2) bottom, feed, and distillate compositions are 0.1, 0.5, and 0.9, respectively; and (3) relative volatility is 2.6. The equilibrium curve is plotted assuming constant relative volatility. The stages are stepped off using the equilibrium curve, the Murphree liquid efficiency method, and the two operating lines in order to determine the number of actual stages or the number of column plates for a given value of the Murphree liquid efficiency.