Applications of Lanchester's Square Law

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
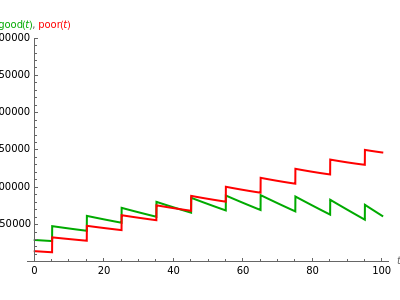
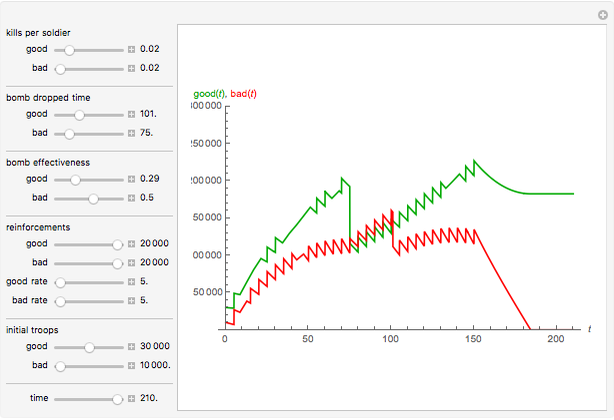
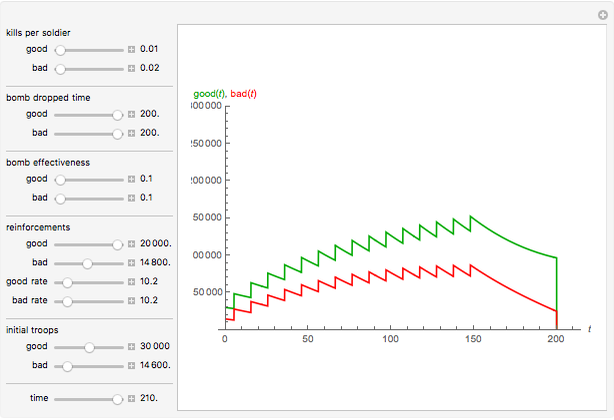
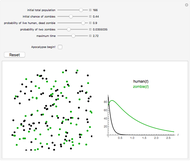
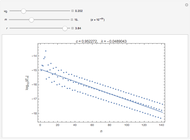
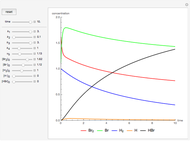
Lanchester's square law models a battle between two armies using a pair of differential equations based on a set of fixed positive constants: the kill rate of good soldiers and the kill rate of poor soldiers. The square law assumes the rate of attrition for one army is solely based on the population and strength of the other army's soldiers, that there is no crossfire where two opposing troops kill each other at the same time and every shot kills only one soldier.
Contributed by: Akash Mukherjee (June 2017)
Additional contributions by George Beck
Based on programs by Eric W. Weisstein
Open content licensed under CC BY-NC-SA
Snapshots
Details
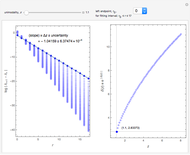
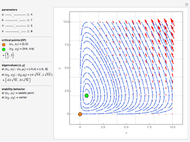
Lanchester's square law states that
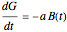 ,
,
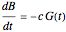 .
.
In addition to Lanchester's square law, this Demonstration has more components—for example:
1. Troops are airlifted in at a specified rate for a certain number of days until the 150th day, when there are no more fighters to send;
2. Each country can use bombs at their discretion;
3. A nuke is dropped on the 200th day, when the battle has dragged on for far too long for both sides.
Special thanks to the University of Illinois NetMath program and the Mathematics Department at William Fremd High School.
Reference
[1] Wikipedia. "Lanchester's Laws." (Jun 9, 2017) en.wikipedia.org/wiki/Lanchester's_laws.
Permanent Citation