Approach of a System of Particles towards Thermal Equilibrium

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
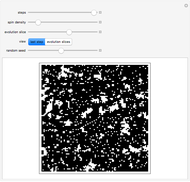
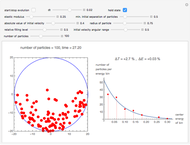
In this simple model, a rigid spherical container contains identical spherical, perfectly elastic particles with the same radius and initially with the same energy. Colliding particles that overlap by  cause a repelling force proportional to
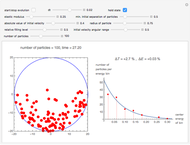
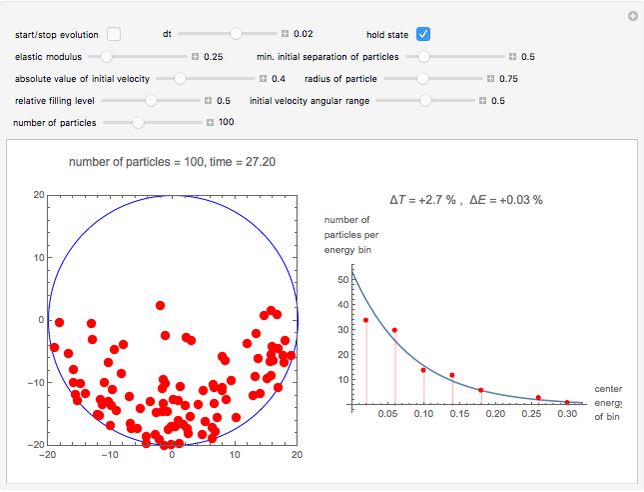
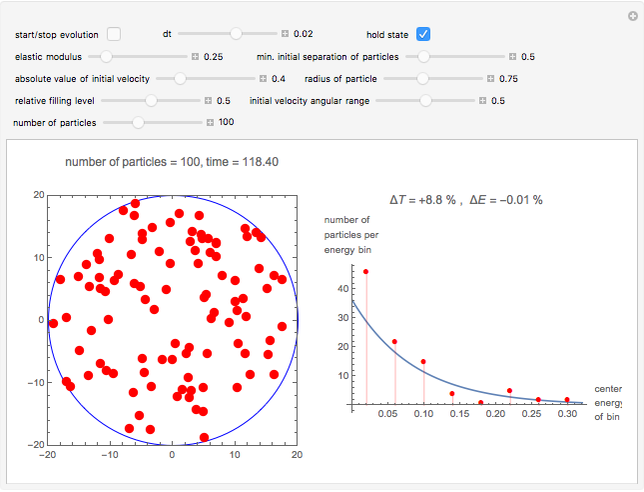
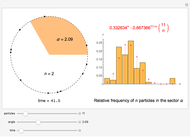
cause a repelling force proportional to 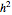 . This redistributes the energy of the collision partners even for binary collisions, where the total energy of the colliding pair remains constant. This redistribution broadens the initially concentrated distribution to an exponential Boltzmann distribution. Such an energy distribution is known from statistical thermodynamics to apply to systems in thermal equilibrium. This Demonstration shows how amazingly fast this energy distribution is attained, although short-lived fluctuations may be observed. Control labels and graphics are explained in tooltips that appear when you mouseover them.
. This redistributes the energy of the collision partners even for binary collisions, where the total energy of the colliding pair remains constant. This redistribution broadens the initially concentrated distribution to an exponential Boltzmann distribution. Such an energy distribution is known from statistical thermodynamics to apply to systems in thermal equilibrium. This Demonstration shows how amazingly fast this energy distribution is attained, although short-lived fluctuations may be observed. Control labels and graphics are explained in tooltips that appear when you mouseover them.
Contributed by: Ulrich Mutze and Stephan Leibbrandt (March 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The total energy of the system is equal to the sum over the energies of the individual particles. The energy of each particle is the sum of its kinetic energy, its potential energy with respect to the wall, and half the sum of its potential energy of interaction with all the other particles. If one forms energy bins using only the kinetic energies (which most textbooks restrict in their treatment of gases), one would approach a Boltzmann distribution in a similar manner, as long as not too many particles overlap with one another or with the wall.
Snapshot 1: sufficiently many collisions have occurred to approach the Boltzmann energy distribution
Snapshot 2: a statistical fluctuation leads us away from the Boltzmann distribution
Snapshot 3: the small size of the particles has prevented a sufficient number of collisions, so we remain far from the Boltzmann distribution
Snapshot 4: a state with maximum number of particles
The autorun feature animates the particle motions, according to the selected options for the initial state.