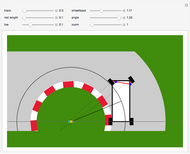
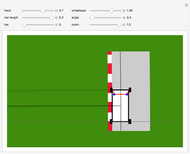
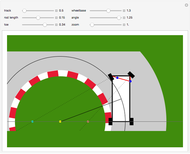
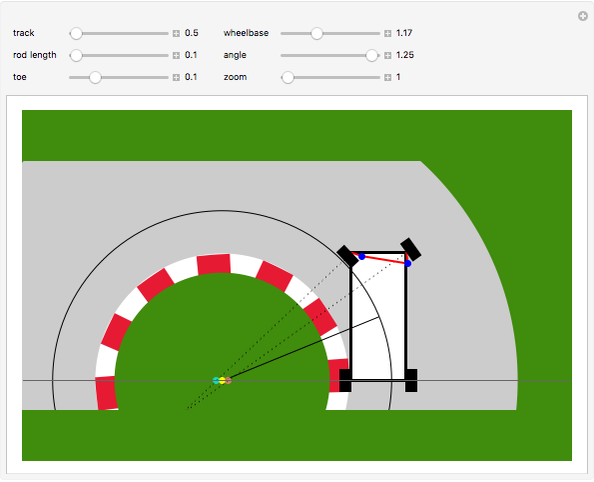
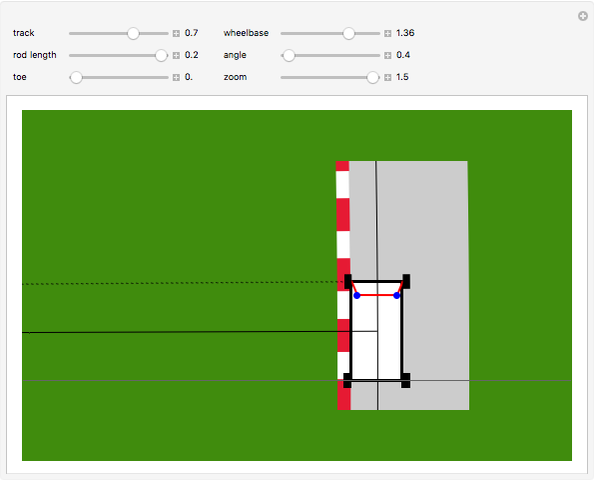
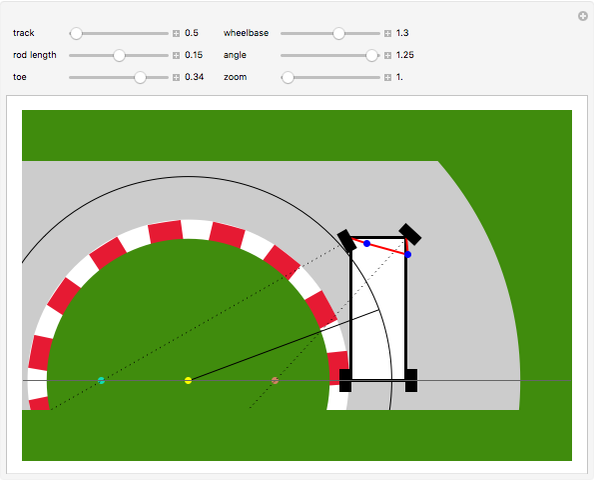
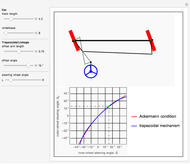
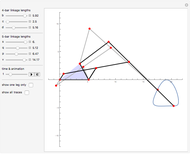
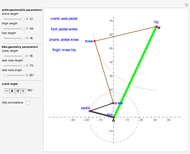
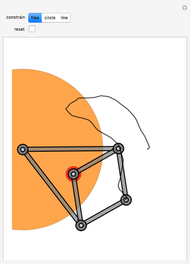
Ackermann geometry is a theoretical model for a steering system that has zero slip. It is achieved when all four wheels of a car are perpendicular to the same turning circle center. This Demonstration uses a common approximation for Ackermann geometry: a simple three-bar linkage. The linkage is arranged in a trapezoid so that the wheel on the inside of a turn will angle more than the outside wheel.