Approximating Pi with Trigonometric-Polynomial Integrals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
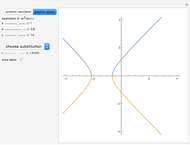
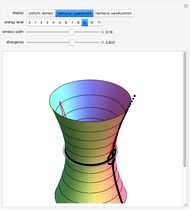
In [1], Frits Beukers invites readers to search for high-quality integral approximations of  . Here, we integrate powers of trigonometric polynomials over the range
. Here, we integrate powers of trigonometric polynomials over the range 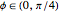 . Integral generating functions satisfy linear differential equations with polynomial coefficients, which lets us generate integral values using linear recurrences with polynomial coefficients. As Doron Zeilberger already notes, these types of equations are exceedingly useful in approximation theory, where they lead to fast calculation of high-order approximants [2]. At least one of the geometric functions,
. Integral generating functions satisfy linear differential equations with polynomial coefficients, which lets us generate integral values using linear recurrences with polynomial coefficients. As Doron Zeilberger already notes, these types of equations are exceedingly useful in approximation theory, where they lead to fast calculation of high-order approximants [2]. At least one of the geometric functions, 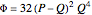 , generates an approximation sequence with asymptotic quality
, generates an approximation sequence with asymptotic quality 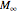 appearing to satisfy
appearing to satisfy 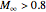 . Not too bad for a number that is notoriously difficult to rationalize.
. Not too bad for a number that is notoriously difficult to rationalize.
Contributed by: Brad Klee (July 2018)
Open content licensed under CC BY-NC-SA
Details
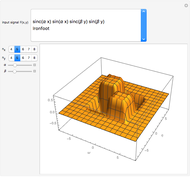
In general, a trigonometric polynomial is an element of a bivariate polynomial ring, 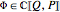 , subject to the following constraints:
, subject to the following constraints:
 ,
,
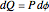 ,
,
 ,
,
which identify 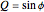 ,
, 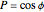 . For
. For 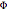 any trigonometric polynomial of degree
any trigonometric polynomial of degree  , we can obtain a normal form by reducing powers of
, we can obtain a normal form by reducing powers of 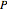 to write
to write
 ,
,
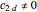 or
or 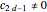 .
.
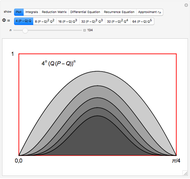
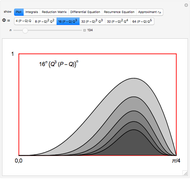
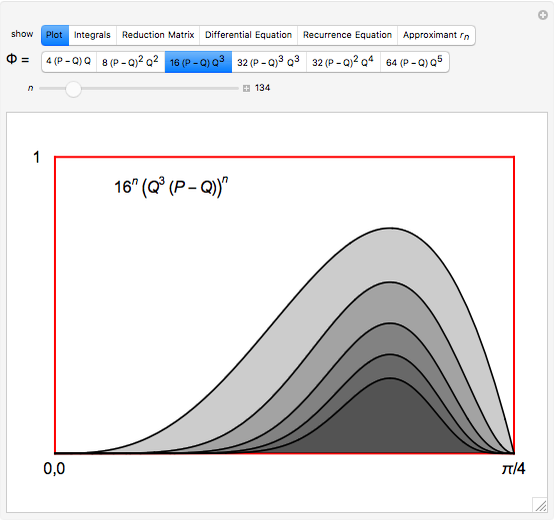
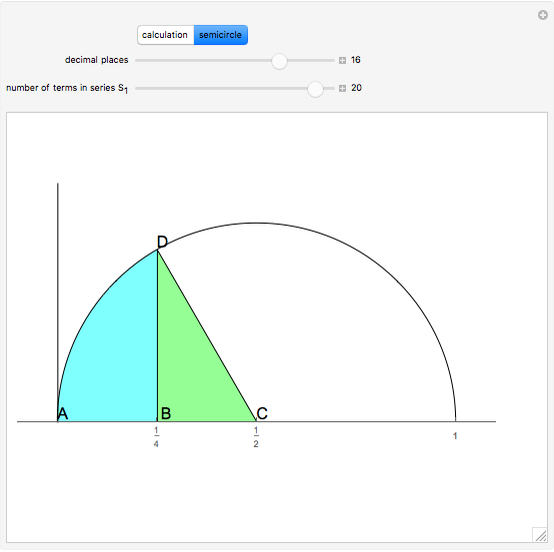
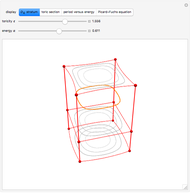
Integrals of the form
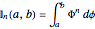
arise in many contexts, including classical physics. Avoiding binomial coefficients and equations of motion, here we focus on cases in which
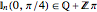 ,
,
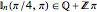 ,
,
 .
.
These conditions allow us to introduce integers 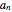 ,
, 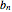 ,
, 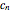 such that
such that
 ,
,
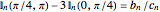 ,
,
with rational identity
 .
.
If 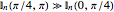 in the limit when
in the limit when  , then clearly
, then clearly 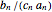 goes to
goes to  simultaneously. These few easy examples are chosen to obviously satisfy the convergence criterion, as
simultaneously. These few easy examples are chosen to obviously satisfy the convergence criterion, as 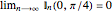 while
while 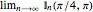 diverges to
diverges to 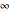 .
.
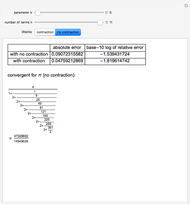
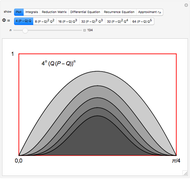
This recipe leads to an infinite set of integral approximations to  , which we would like to start ranking by quality. As in [1], the quality of rational approximant
, which we would like to start ranking by quality. As in [1], the quality of rational approximant  (with
(with 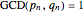 ) is determined by the equation
) is determined by the equation
 , (
, (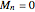 if
if 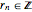 ).
).
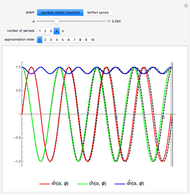
The function 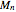 behaves stochastically on the scale of small variations, but overall tends to a stable limit with some variance. We would like to find the value
behaves stochastically on the scale of small variations, but overall tends to a stable limit with some variance. We would like to find the value
 ,
,
but direct integration becomes prohibitively difficult when the degree of  is large. With
is large. With 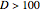 , integration time already reaches the 1(s) scale. Fortunately, we have a general solution to the problem of quickly computing high-order terms, which reduces iteration to a linear calculation.
, integration time already reaches the 1(s) scale. Fortunately, we have a general solution to the problem of quickly computing high-order terms, which reduces iteration to a linear calculation.
Every trigonometric polynomial 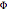 contributes to an integral generating function
contributes to an integral generating function
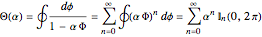 ,
,
with formal parameter  . Period
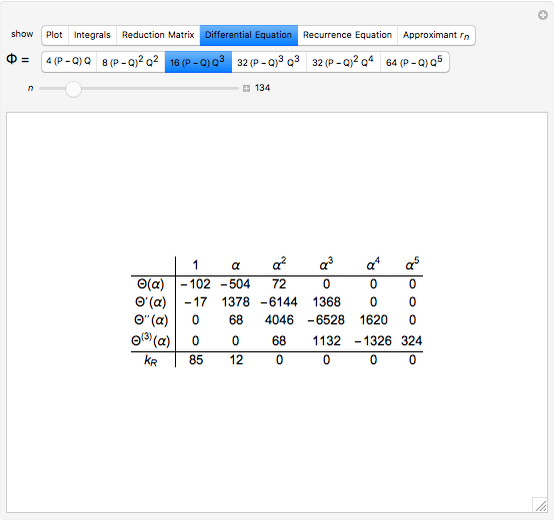
. Period 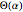 is a rational integral, so satisfies a linear differential equation [3],
is a rational integral, so satisfies a linear differential equation [3],
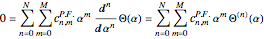 ,
,
with 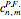 a matrix of integers.
a matrix of integers.
The source code contains a degree-bounded algorithm TrigPicardFuchs that must return a positive result with 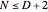 . We omit details of the proof here, but emphasize that the top-left block of the check matrix is always nondegenerate, which guarantees solvability and halting on success for any trigonometric polynomial
. We omit details of the proof here, but emphasize that the top-left block of the check matrix is always nondegenerate, which guarantees solvability and halting on success for any trigonometric polynomial 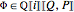 . The outputs can be checked against HolonomicFunctions'Annihilate [4]. In timing tests, TrigPicardFuchs competes quite well against Annihilate.
. The outputs can be checked against HolonomicFunctions'Annihilate [4]. In timing tests, TrigPicardFuchs competes quite well against Annihilate.
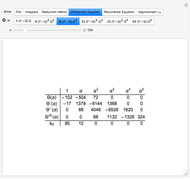
Once the differential equation is known, we can rigorously derive nonlinear recurrences,
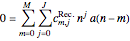 ,
,
usually determining the integers 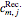 by validating guessed recursions against the Frobenius method (see Frobenius Method (Wolfram MathWorld)).
by validating guessed recursions against the Frobenius method (see Frobenius Method (Wolfram MathWorld)).
Finally, if we redefine 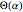 as an integral over the interval
as an integral over the interval 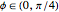 , the differential equation must be modified to nonhomogeneous form,
, the differential equation must be modified to nonhomogeneous form,
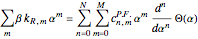 ,
,
where the coefficients 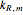 account for the rational part of
account for the rational part of 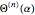 , only up to a sign and scale given by the free parameter
, only up to a sign and scale given by the free parameter 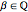 . We call the
. We call the 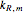 a checksum of the integral approximation.
a checksum of the integral approximation.
These calculations take us through some fun areas of mathematics, but we should not delay the data analysis. Iterating to  , it seems that our approximation
, it seems that our approximation 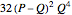 reaches a higher quality than
reaches a higher quality than 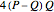 , which appears in Beukers's article and in the On-Line Encyclopedia of Integer Sequences (cf. A006139 [5]).
, which appears in Beukers's article and in the On-Line Encyclopedia of Integer Sequences (cf. A006139 [5]).
To certainly reach  , we must work with a more complicated integral,
, we must work with a more complicated integral,
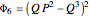 ,
,
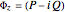 ,
,
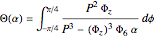 .
.
This integral is Beukers's final example, and also appears in the On-Line Encyclopedia of Integer Sequences alongside the appropriate differential equations and linear recurrences (cf. A123178, A305997 and A305998 [6–8]). More work remains to be done. In particular, will a trigonometric polynomial ever lead to an approximation of 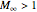 ?
?
References
[1] F. Beukers, "A Rational Approach to Pi," Nieuw archief voor wiskunde, Serie 5, 1(4), 2000 pp. 372–379. (Jul 24, 2018) dspace.library.uu.nl/handle/1874/26398.
[2] S. B. Ekhad and D. Zeilberger, "Searching for Apery-Style Miracles [Using, Inter-Alia, the Amazing Almkvist-Zeilberger Algorithm]." arxiv.org/abs/1405.4445.
[3] P. Lairez, "Computing Periods of Rational Integrals," Mathematics of Computation, 85, 2016 pp. 1719–1752. doi:10.1090/mcom/3054.
[4] C. Koutschan. "HolonomicFunctions: A Mathematica Package for Dealing with Multivariate Holonomic Functions, Including Closure Properties, Summation, and Integration." (Jul 24, 2018) www.risc.jku.at/research/combinat/software/ergosum/RISC/HolonomicFunctions.html.
[5] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. oeis.org/A006139.
[6] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. oeis.org/A123178.
[7] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. oeis.org/A305997.
[8] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. oeis.org/A305998.
Snapshots
Permanent Citation