Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

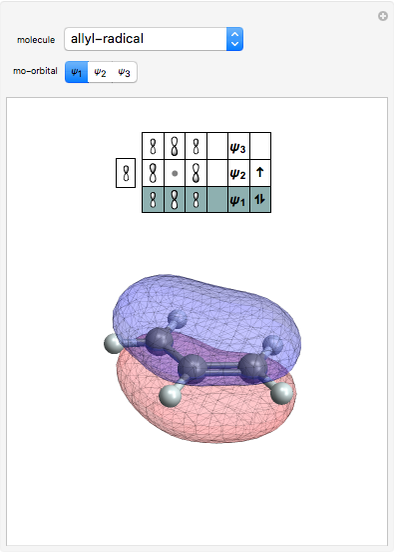
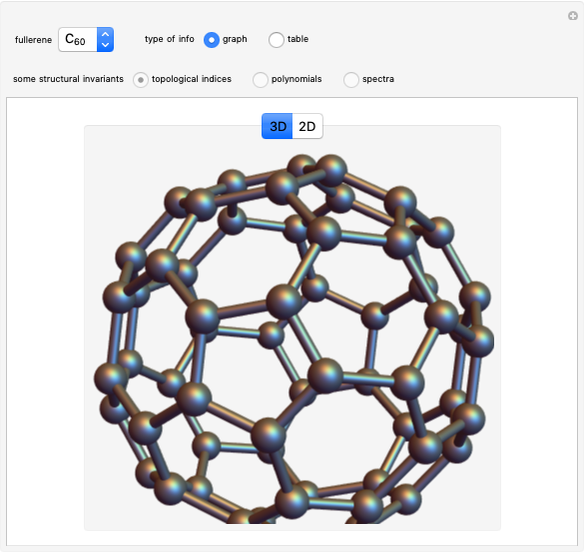
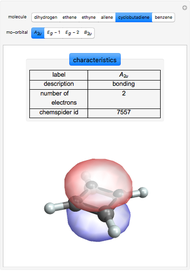
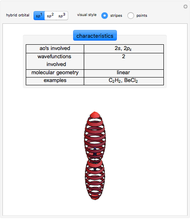
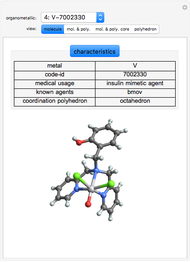
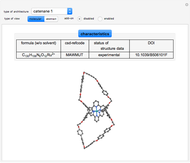
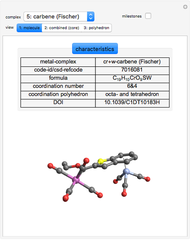
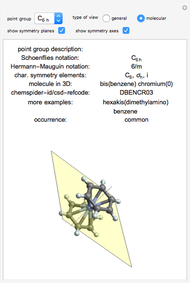
Architectural Applications of Several 3D Geometric Transformations

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

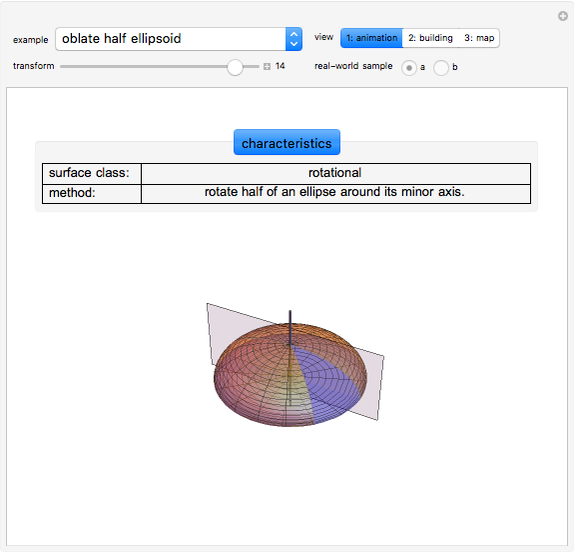
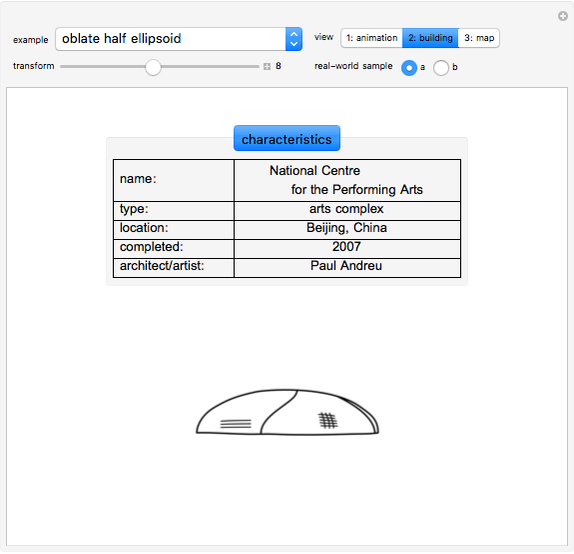
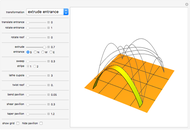
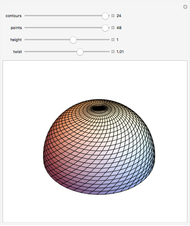
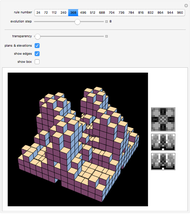
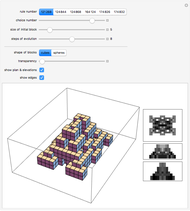
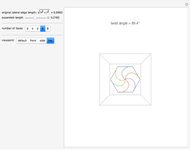
This Demonstration considers the following surfaces: ellipsoid, hyperboloid of one sheet, elliptic paraboloid, hyperbolic paraboloid, helicoid, and Möbius strip, which can be represented by parametric equations of the general form 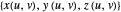. These surfaces can undergo further transformations, including rotation, translation, helical motion, and ruling.

[more]

To illustrate the application of these methods in architecture, sketches of real-world examples are displayed, as well as maps showing their locations.

This Demonstration shows a set of six structures: their animated transformation in 3D, one or two matching sketches of a building, and a map for each of the six 3D surfaces. Short descriptions or legends for each graphic are given.

[less]

Contributed by: Guenther Gsaller (February 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

$Failed
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send