Area of a Triangle in the Poincaré Disk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
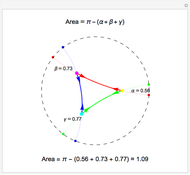
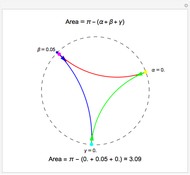
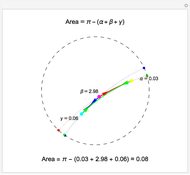
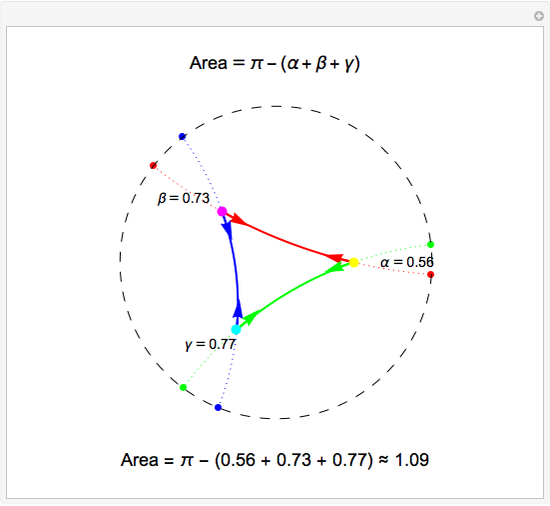
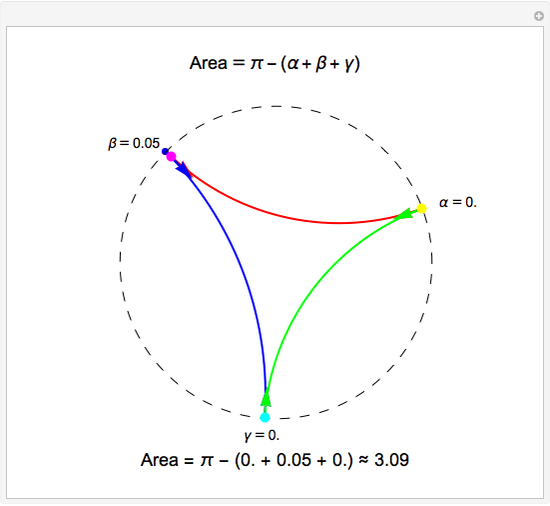
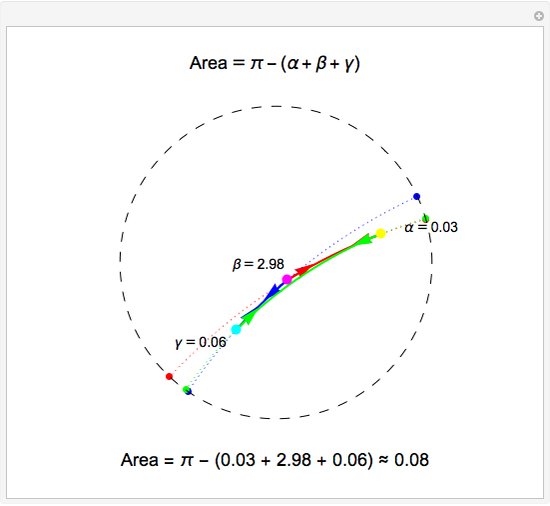
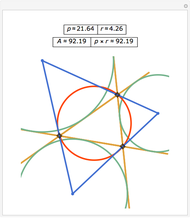
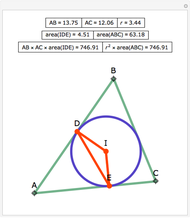
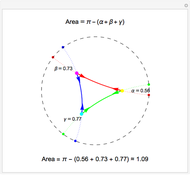
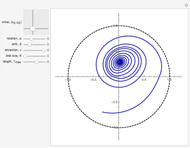
This Demonstration shows a triangle formed by three geodesics in the Poincaré disk. At each vertex, tangent vectors to the two intersecting geodesics are shown. The angle in radians between each pair of vectors is displayed and labeled as  ,
, 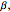 or
or  per the Gauss-Bonnet formula for the area of a hyperbolic triangle, which is shown above the disk. The boundary of the disk is dashed to indicate that the boundary is not part of the Poincaré disk. Below the disk, the area is computed approximately. Notice that if all three vertices are "infinite" vertices (vertices on the boundary circle) the area of the triangle is
per the Gauss-Bonnet formula for the area of a hyperbolic triangle, which is shown above the disk. The boundary of the disk is dashed to indicate that the boundary is not part of the Poincaré disk. Below the disk, the area is computed approximately. Notice that if all three vertices are "infinite" vertices (vertices on the boundary circle) the area of the triangle is  .
.
Contributed by: Steven Broad (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Poincaré disk is a model of hyperbolic space. Geodesics in the Poincaré disk model are of two types:
1. The intersection of a line through the origin and the open disk.
2. The intersection of a circle not through the origin that intersects the boundary of the disk orthogonally.
Given any two points in the Poincaré disk, there is a unique geodesic that passes through both of them. Hence, if two points are given and a third point is chosen that is not contained in the geodesic determined by the first two, these three points determine a unique hyperbolic triangle.
Hyperbolic space has a metric that confers a constant curvature of  . In the Poincaré disk model the metric tensor is
. In the Poincaré disk model the metric tensor is
 .
.
The Gauss-Bonnet theorem applied to this metric on the boundary of the triangle gives a formula for the area of the hyperbolic triangle, namely
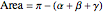 ,
,
where  ,
, 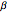 , and
, and  are the measures of the interior angles of the triangle. It is worth pointing out that the sum of the interior angles of a hyperbolic triangle must be less than
are the measures of the interior angles of the triangle. It is worth pointing out that the sum of the interior angles of a hyperbolic triangle must be less than  (which is quite different from Euclidean geometry, in which that sum must equal
(which is quite different from Euclidean geometry, in which that sum must equal  ).
).
References:
J. W. Anderson, Hyperbolic Geometry, New York: Springer-Verlag, 1999 pp. 95–104.
S. Katok, Fuchsian Groups, Chicago: University of Chicago Press, 1992.
Permanent Citation