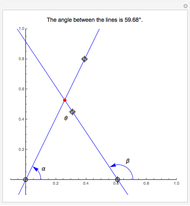
Area of a Triangle Using Sine

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
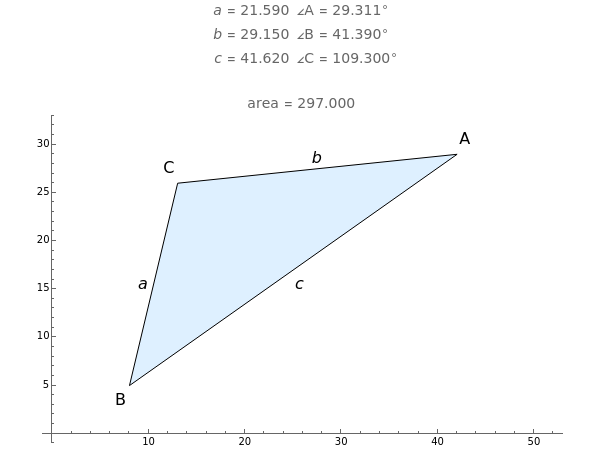
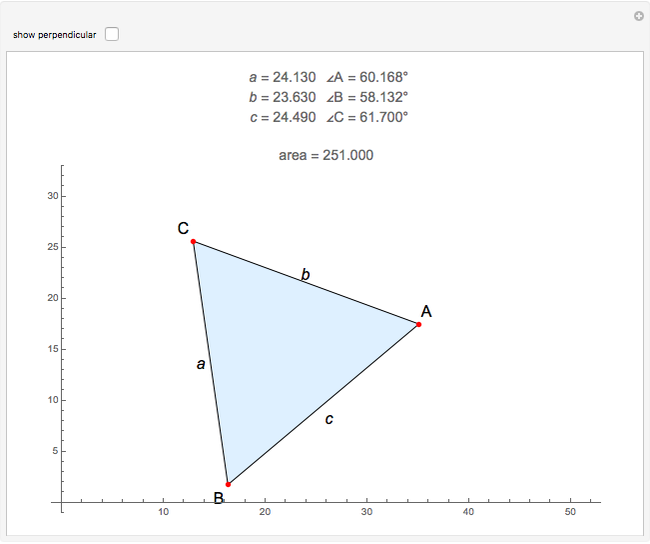
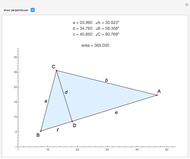
Let the triangle 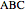 have side lengths
have side lengths 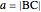 ,
, 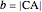 and
and 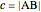 . Then the area is
. Then the area is 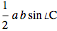 . A proof is outlined in the Details.
. A proof is outlined in the Details.
Contributed by: Enrique Zeleny (July 2018)
Open content licensed under CC BY-NC-SA
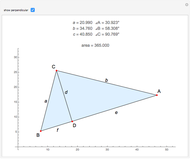
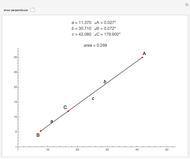
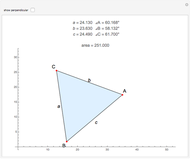
Snapshots
Details
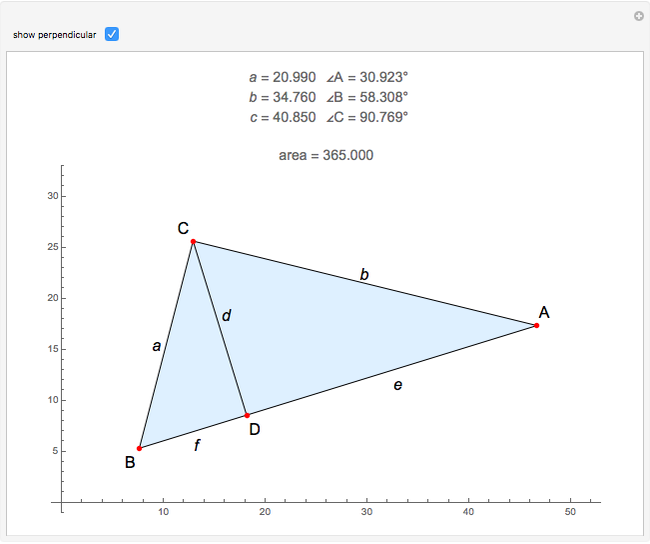
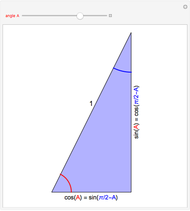
Here is a derivation of the formula. Draw a perpendicular from the point  to the side
to the side  at
at 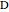 . The triangle
. The triangle 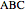 is now divided into two right triangles
is now divided into two right triangles 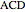 and
and 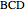 . Let
. Let 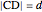 . Let the lengths of the two segments of
. Let the lengths of the two segments of  be
be  and
and 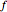 .
.
Then, by trigonometry, 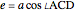 ,
,  ,
,  . (*)
. (*)
The area of the triangle is

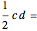 (the base is
(the base is  and the height is
and the height is  )
)
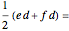 (
(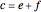 )
)
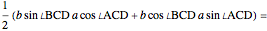 (substituting from (*))
(substituting from (*))
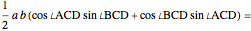 (factoring out
(factoring out 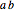 )
)
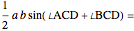 (using the expansion of the sine of a sum in reverse)
(using the expansion of the sine of a sum in reverse)
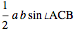 . (adding the two angles at
. (adding the two angles at  )
)
Permanent Citation