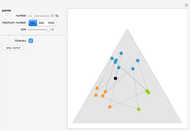
Attractors of Iterated Affine Transform Systems

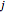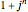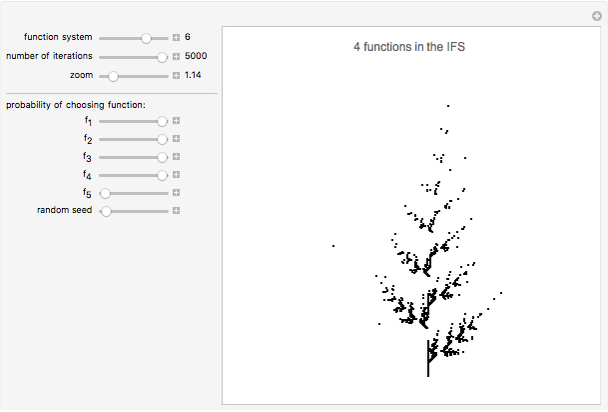
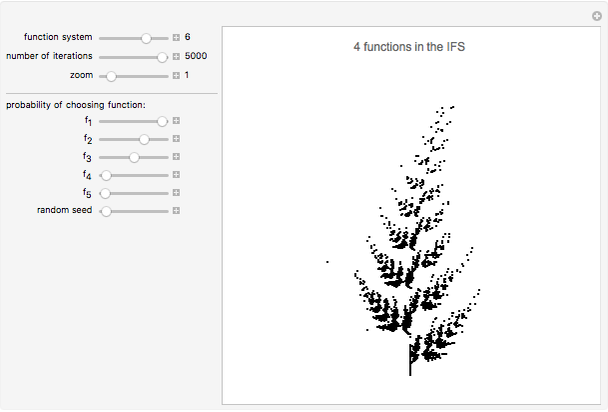
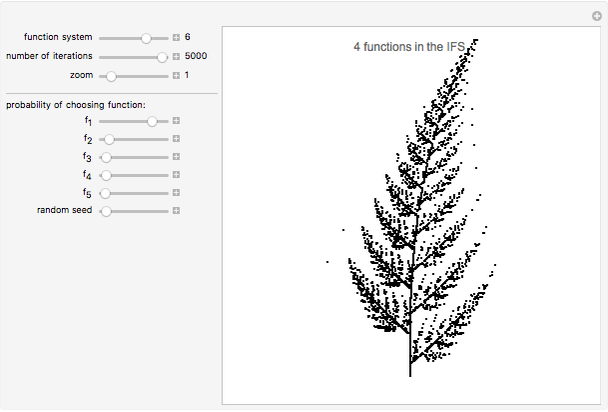
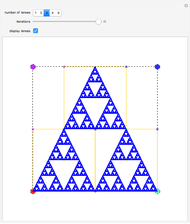
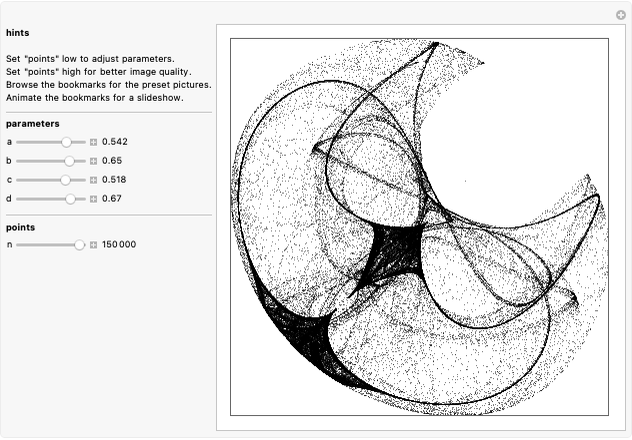
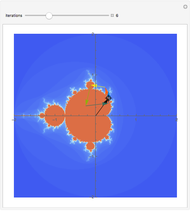
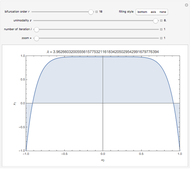
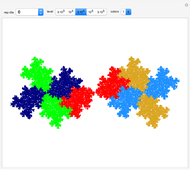
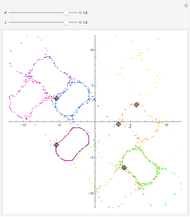
An iterated function system (IFS) maps a set of affine transforms on a point and the resulting images repeatedly. If the system contains functions, there are points after iterations and the number of points grows exponentially. To reduce the volume of data, instead of applying all of the functions of the system at each step, only one is chosen, according to some given probability. This Demonstration shows how the attractors for eight particular systems emerge as you increase the number of iterations. There are two astonishing things about IFS: first, the attractor does not depend on the initial point; second, the probabilities for each transform can concentrate the points in certain regions and improve the picture. Fractal structures can be explored with the zoom control.